Pyramid Path :
Difficulty Level : Medium
Submissions : 601
Asked In :
Marks :10
: 11 | : 1
Your goal is to find the maximum path value of viable paths in a pyramid. A viable path is one were you take either one step to the left or right as you progress down the nodes of the pyramid. You must pass through every level. The total path value is the sum of the values in the nodes traversed by your path. The diagram below represents a simple 3-layer pyramid with 4 possible paths:
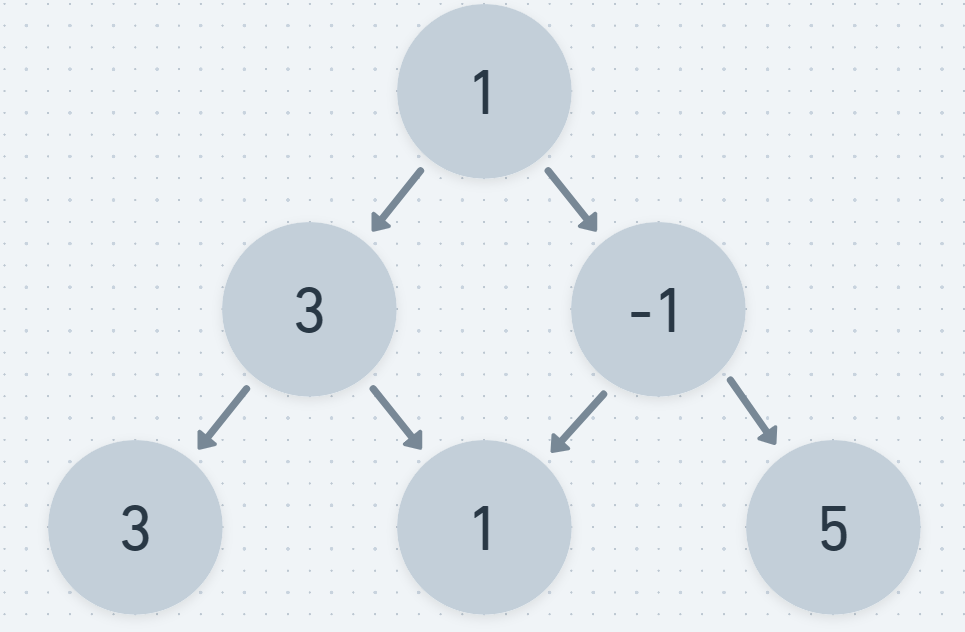
In the above example, the correct answer is 7
The pyramid input will be given in the level order traversal flattened into a 1D array.
For the above example, so you will receive an array [1, 3, -1, 3, 1, 5] as input.
A single letter N corresponding to the size of the array followed by the next line containing N space separated integers corresponding to the cost of the $$$i_{th}$$$ node.
$$$1 \le N \le 1000000 $$$
$$$-10^9 \le cost_i \le 10^9 $$$
It is guaranteed that the number of nodes represents a complete pyramid.
example : 1 , 3 , 6 , 10 ...and so on.
A single integer value corresponding to the maximum cost.
6 1 3 -1 3 1 5
7
