14 months ago

sober 100

Mumbai

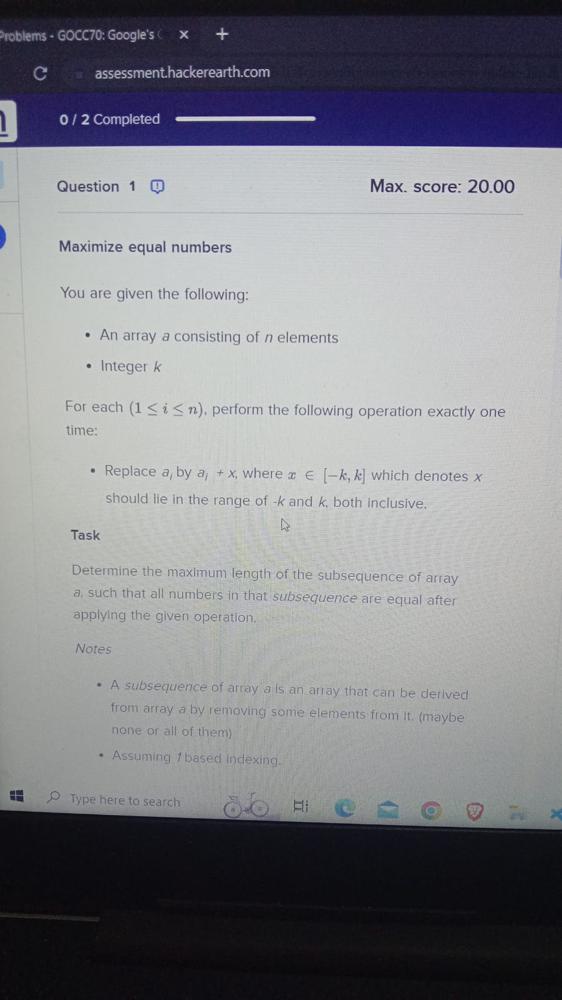
Q1. Maximize Equal Numbers

You are given the following :

• An array a consisting of n elements
• Integer k

For each (1 ≤ i ≤ n ) perform the followingoperation exactly one time :

• Replace a_i  by a_i + x , where x ∈ [-k , k ] which denotes x should lie in the range of -k to k both inclusive

Task

Determine the maximum length of subsequence of array a , such that all numbers in the subsequence are equal after applying the given operations 

Notes

• A subsequence of array a is an array that can be derived from array a by removing some elements  from it (maybe none or all of them)
• Assuming 1 based indexing

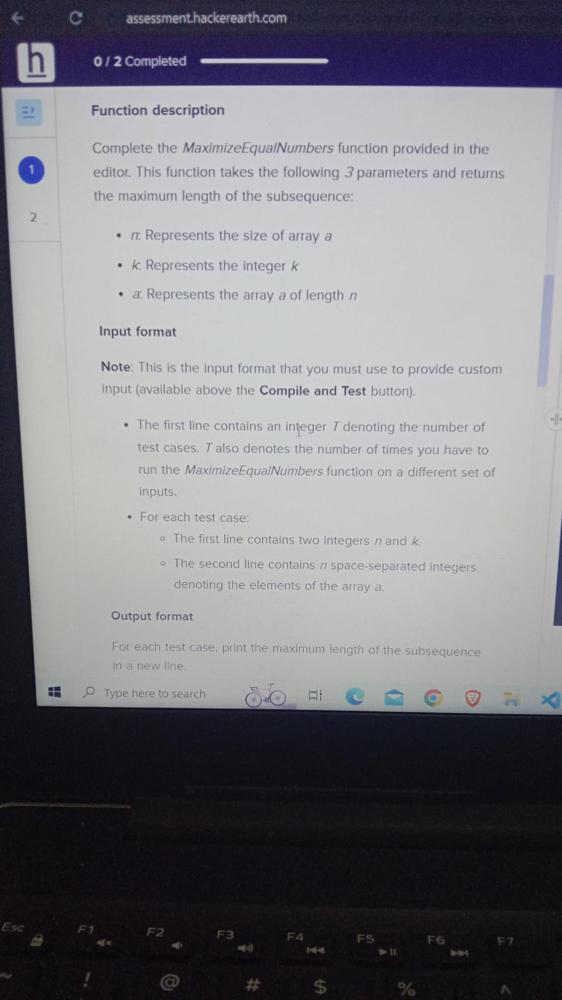
Function description 

Complete the MaximizeEqualNumbers functionprovided in the editor . This function takes 3 parameters and returns the maximum length of the subsequence 

• n : Represents the size of array a 
• k : Represents the integer k
• a : represents the array a of length n

Input format

Note: This is the input format that you must use to provide cuxtom input(available above the compile and test button)

• The first line contains an integer T denoting the number of test cases . T also denotes the number of times you have to run the MaximizetheequalNumbers function on a different set of inputs
• For each test case :
  • first line contains two integers n and k 
  • the second line contains n space-sepparated integers denoting the elements of the array a 

Output format

For each test case, print the maximum length of the susequence in new line .

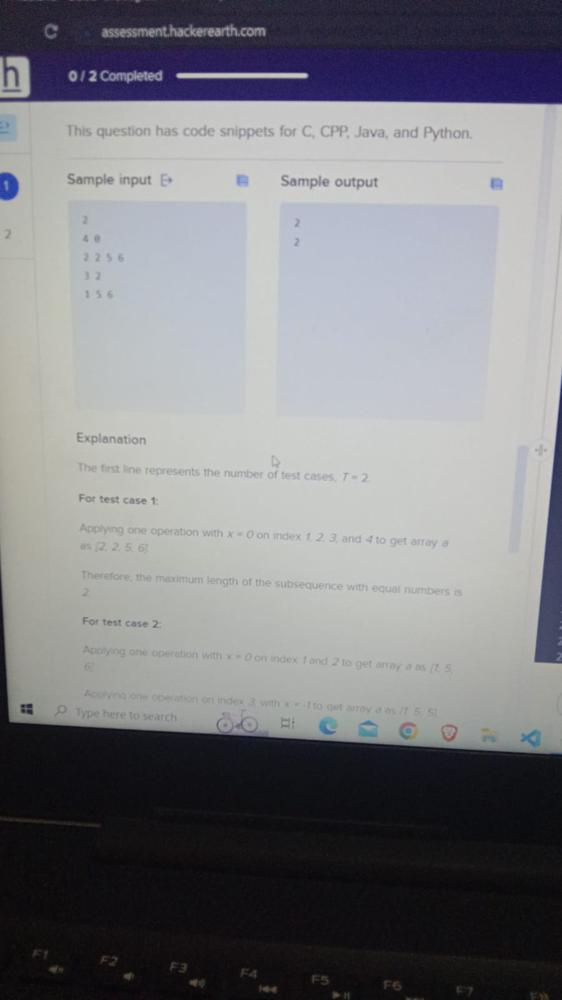
The question has code snippets from CPP , Python , C and Java

Sample Input                   Sample Output
2                                            2
4 8                                         2
2 2 5 6
3 2 
1 5 6

 Explanation

The first line represents the number of test cases T=2

For test case 1:

 Applying one operation with x= 0 on index 1,2,3 and 4 to get array a as [ 2, 2, 5, 6]

Therefore , the maximum length if the subsequence with equal numbers as a
2

For test case 2:
Applying one operation i with x = 0 on index 1 and 2 to get array a as [1,5,6]
Applying one operation on index 3 iwth x= 1 to get array a as [1,5,5]


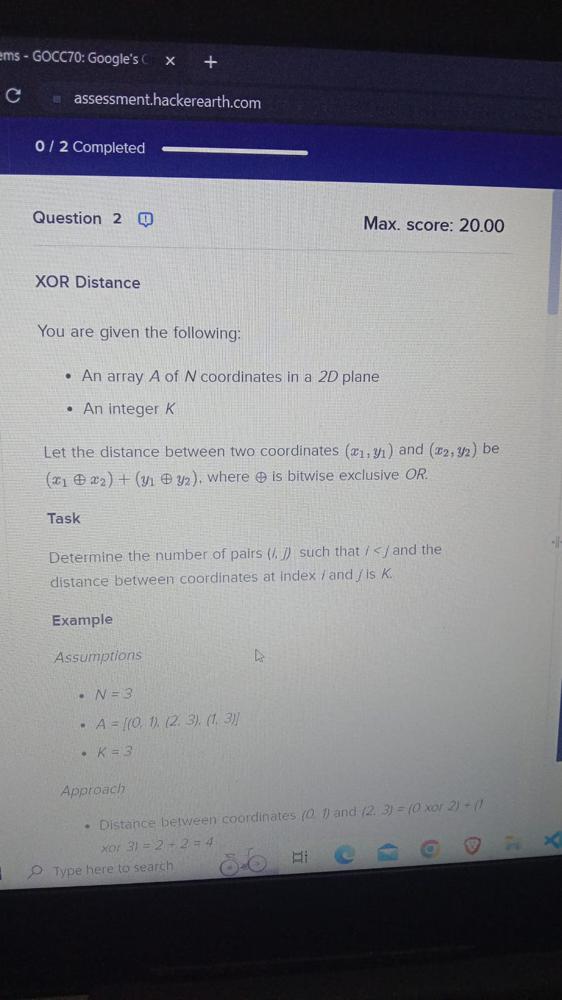
Q2. XOR Distance

• You are given an array A of N coordinates in a 2D plane
• An integer K 

Let the distance between two coordinates (x₁,y₁)  and (x₂,y₂) be (x₁ ⊕ x2) +  (y₁ ⊕ y₂) , where ⊕is bitwise exclusive OR

Task

Determine the number of pairs (i,j) such that  i,j and the distance between coordinates at index i and j is K 

Example 

Assumption 

• N = 3
• A = [(0,1),(2,3),(1,3)]
• K = 3

Approach 

• Distance between coordinates (0,1) and (2,3) = (0 xor 2) + (1 xor 3) = 2+2=4
   

The question has code snippets from CPP , Python , C and Java

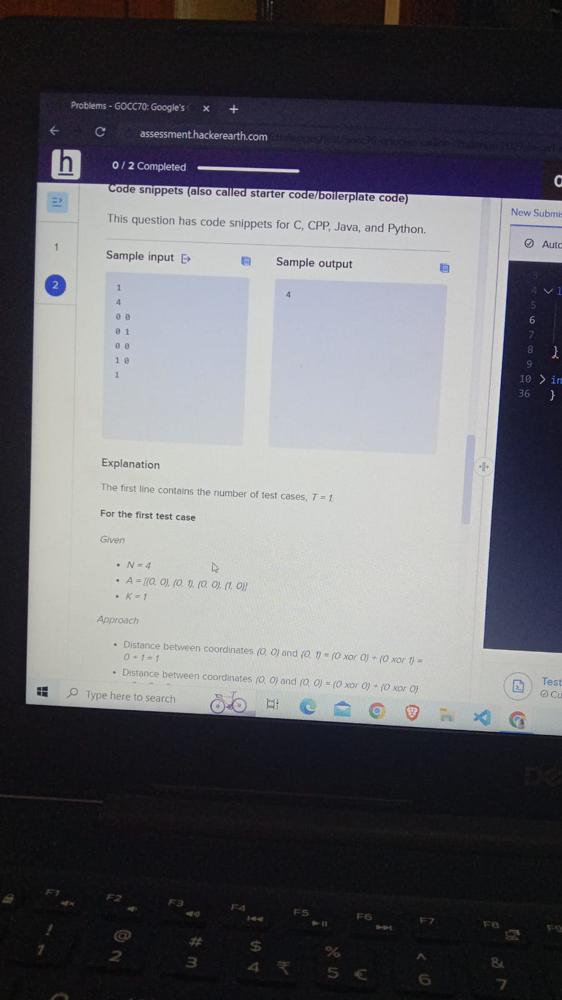
Sample Input                   Sample Output
1                                               4
4
0 0 
0 1 
0 0
1 0
1

Explanation 

The first line contains the number of test cases  , T = 1

For the first test case 

Given 

• N = 4
• A = [(0,0), (0,1) ,(0,0) , (1,0)]
• K = 1

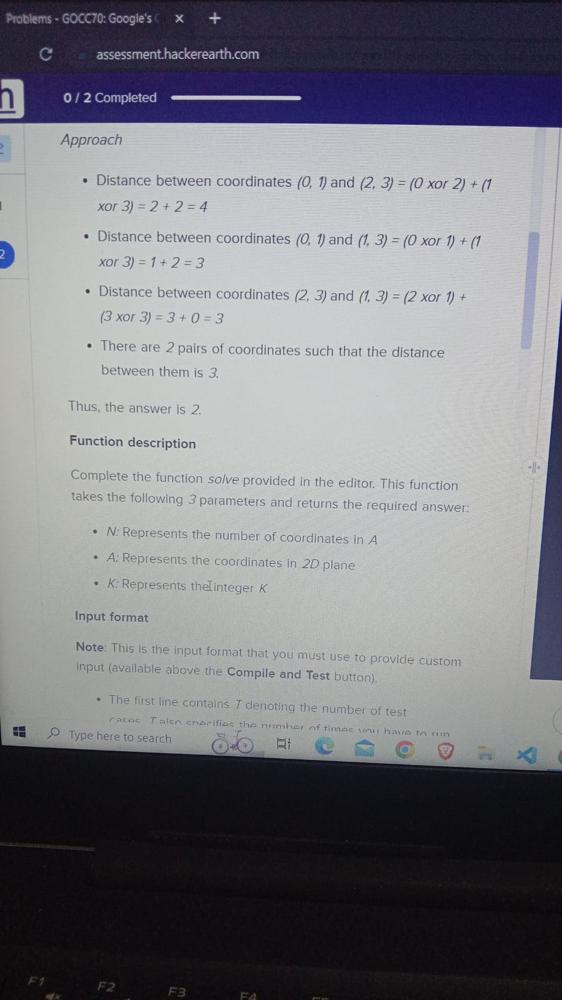
Approach 

• Distance between coordinates (0, 1) and (1, 3) = (0 xor 1) + (1
  xor 3) = 1 + 2 = 3
• Distance between coordinates (2,3) and (1, 3) = (2 xor 1) + (3 xor 3) = 3 + 0 = 3

There are 2 pairs of coordinates such that the distance between them is 3.
Thus, the answer Is 2.

Function description
Complete the function solve provided in the editor. This function takes the following 3 parameters and returns
The required answer:

• N: Represents the number
• of coordinates in A
• A: Represents the coordinates in 2D plane
• K: Represents the integer K
• Input format
   

Note:
This is the input format that you must use to provide custom input (available above the Compile and Test button).

• The first line containsdenoting the number of test

= 

Q2. XOR Distance

3 months ago

slime • 350

Hyderabad

[P1] Maximize Equal Numbers

Brief

Given N integers and an integer K, you are allowed to increase each integer by X, where X belongs to [-K, +K].
You want to make maximum numbers equal after modifying each of N numbers.

Solution

i^th number after modification will lie in range [A_i - K, A_i + K].
Thus, instead of viewing each number as a single point on number line, we can view it as a range.
Problem thus reduces to finding point on number line where maximum number of ranges overlap.

Example #1
   A = [5, 7, 10, 8, 15]
   K = 4

After modifying 5, it will be in range [1, 9]
After modifying 7, it will be in range [3, 11]
After modifying 10, it will be in range [6, 14], and so on..
This is represented by diagram below:-

Let Z be one of integers where maximum ranges overlap. For example above Z could be either of 8 or 9 where all 5 ranges overlap.
Thus, it is possible to convert all integers in array to either 8 or 9, that results in required answer as 5.

To verify, we can see adding +3 to 5, +1 to 7, -2 to 10, +0 to 8, and -4 to 12 results in array [8, 8, 8, 8, 8].

So how do we find this maximum overlapping ranges amongst given N ranges?

1. Simply insert into vector, for each range its starting and ending point along with flag whether they are starting or ending point.
   For above example, this will result in {(S,1), (E, 9), (S, 3), (E, 11) .... (S, 8), (E, 16)}.
2. Sort this vector by integer in each pair inserted in vector.
3. Initialize variable current = 0
4. Now evaluate each pair in ascending order:-
   1. increment current by 1when you encounter pair of type S (starting point), and
   2. decrement current by 1 when you encounter pair of type E (ending point)
5. This essentially simulates us sweeping a line from left to right and counting current number of ranges overlapping!
6. Maximum value of variable currentis the required answer.

Code

int solve(vector<int> &A, int K) {
	vector<pair<int,int>> sweep;
	for (auto x: A) {
		sweep.push_back({x-K, 0}); //0 -> flag for starting point
		sweep.push_back({x+K, 1}); //1 -> flag for ending point
	}
	sort(sweep.begin(), sweep.end());
	int ans = 0, current = 0;
	for (auto x: sweep) {
		if (x.second == 0) current++; else current--;
		ans = max(ans, current);
	}
	return ans;
}

3 months ago

slime • 350

Hyderabad

Here is solution for P2 as well on request by @Abhishek.

[P2] XOR Distance

Let's use technique taught in class, solve 1D version of this problem and then extend its intuition to 2D.

1D SubProblem

Given array of N integers, and an integer K, find number of ordered pairs whose XOR = K.

To solve this, we need to understand that for any given integer say X, there exists a unique integer Y, such that X ⊕ Y = K. (Think bit-by-bit and this will make sense).

Now, lets say for A_i, we want to find number of A_j such that A_i ⊕A_j = K for j < i.
This is easy, since A_i ⊕ K will give you value of A_j !! All you need to check is how many A_j exists whose value is A_i
 ⊕K. (This you can use unordered_map to keep track of).

Thus you can solve this problem in O(N).

Original 2D Problem

Extending intuition, we can find out for (X_i, Y_i) how many (X_j, Y_j) exists for j < i whose XOR is K. How?
Lets say for some integers m and n, X_i ⊕m + Y_i ⊕n = K is true. What all can be m, n?

It can be one of following K+1 cases:-
  Case #1 : X_i ⊕ m = 0 and Y_i ⊕ n = K. (This uniquely determines n, m)
  Case #2 : X_i ⊕ m = 1 and Y_i ⊕ n = K-1. (This uniquely determines n, m)
  Case #3 : X_i ⊕ m = 2 and Y_i ⊕ n = K-2. (This uniquely determines n, m)
  ....
  Case #K+1 : X_i ⊕ m = K and Y_i ⊕ n = 0. (This uniquely determines n, m)

Thus, find all possible points that you have seen so far (again using unordered_map) where n, m has values as one of above cases.
K <= 100, N <= 10⁵ in given question. So this makes our solution as O(K.N) 

14 months ago

sober 100

Mumbai

Code for 2nd problem 
XOR DISTANCE
credit : @slime

#include <bits/stdc++.h>
using namespace std;

#ifndef ONLINE_JUDGE
#define debug(x) cerr << #x <<" "; _print(x); cerr << endl;
#else
#define debug(x)
#endif

int main() {

#ifndef ONLINE_JUDGE
	freopen("input1.txt", "r", stdin);
	freopen("output1.txt", "w", stdout);
	freopen("Error.txt", "w", stderr);
#endif


	int t;
	cin >> t;
	while (t--)
	{
		int n, k;
		cin >> n;

		vector<pair<int, int>>v(n);
		for (int i = 0; i < n; i++) {
			cin >> v[i].first >> v[i].second;
		}
		cin >> k;

		int ans = 0;
		map<pair<int, int>, int>mp;
		for (auto it : v) {

			int x = it.first;
			int y = it.second;

			for (int j = 0; j <= k; j++) {

				int a = j;   // a = x1 ^ x2
				int b = k - a; // b = y1 ^ y2

				//extracting x2,y2
				int x2 = a ^ x;
				int y2 = b ^ y;

				if (mp.find({x2, y2}) != mp.end()) {
					ans += mp[ {x2, y2}];
				}
			}

			mp[ {x, y}]++;
		}

		cout << ans << endl;

	}
	return 0;
}