5 weeks ago

John 910

Hyderabad

Question 1

You are given a string S of length N, which contains only lowercase alphabets from 'a' to 'z'.

Let's define the score of a string as xor of the occurrence of each character in the string.

You are required to handle two types of queries

• 1 L R: You need to answer the score of the substring of S from L to R
• 2 X Y: Update the character at position X to Yth alphabet from 'a' to 'z'

Notes

• 1-based indexing is followed.
• The XOR operation takes two numbers as operands and does XOR on every bit of two numbers. The result of XOR is 1 if the two bits are different, otherwise, it is 0.
• Yth alphabet from 'a' to 'z' is the character at Ythindex (1-based) in string 'abcdefghijklmnopqrstuvwxyz'. For example, 4th alphabet is 'd'.
• A substring of a string is a contiguous subsequence of that string.

Task

For each query of type 1, output the score of the string.

Example

Assumptions

• S = 'abda'
• Q = 2
• queries = [[2,3,2],[1,1,3]]

Approach

• The first query

   Update 3rd index from left to 2nd alphabet from 'a' to 'z'. So we can change from 'a' to 'b'. The resulting string is 'abba'
  

• The second query

   The substring from 1 to 3 is abb. The frequency of character 'a' is 1 and the frequency of character 'b' is 2.
  
   Thus, the score of the substring is 1 *XOR* 2 = 3
  

Constraints

1 <= |T| <= 10

2 <= |S| <= 10^5

1 <= Q <= 10^5

1 <= L <= R <= |S|

1 <= X <= |S|

1 <= Y <= 26

Sample Input

1
tti
4
2 3 1
1 1 2
2 1 2
1 2 3

Sample Output

2   0

Question 2

Good String

Good string 

You are given a string S of length N, Q ranges of the form [L. R] in a 2D
array range. and a permutation arr containing numbers from 1 to N.

Task

in one operation, you remove the first unremoved character as per the permutation. However, the positions of other characters will not change.
Determine the minimum number of operations for the remaining string to be good.

Notes

• A string Is considered good if all the Q ranges have all distinct characters, Removed characters are not counted,
•  A range with all characters removed is considered to have all distinct characters
•  The sequence of n integers is called a permutation if it contains all Integers from 1 to n exactly once
• I-based Indexing Is followed

Example

Assumptions

* N=5 Q=2 S= "aaaaa"
arr=[2,4,1,3, 5]
ranges = [[1,2],[4,5]]

Approach

• After the first operation, the string becomes a_aaa
• After the second operation, the string becomes a_a_a
• Now, in both ranges, all characters are distinct

Hence, the output is 2
Function description

Complete the goodString function provided in the editor. This function
takes the following 6 parameters and retums the minimum number of
operations:

•  N Represents the length of the string
•  S: Represents the string
• arr. Represents the permutation according to which characters will be removed
• Q Represents the number of ranges
• ranges: Represents an array of 2 integer armays describing the ranges [L,R] which should have all distinct characters

Input Format

This is the input format that you must use to provide custom input
above the Compile and Test button).

• The first line contains a single integer T denoting the number of
• test cases. T also specifies the number of times you have to run
• the goodsString function on a different set of Inputs,
• For each test case:
  •  The first line contains 2 space-separated integers Nand Q.
  •  The second line contains the string S. Xs
  • The third line contains N space-separated integers denoting the permutation arr.
  •  Each of the Q following lines contains 2 space-separated Integers describing the range, L and R

For each test case , print a single integer in a single line  denoting the minimum number of operations required for the remaining string to be good

Constraints 

1 ≤  T ≤ 10

1 ≤ N ≤ 10⁵

1 ≤ Q ≤ 10⁵

1 ≤ arr_i ≤ N

1 ≤ L_i ≤  R_i ≤ N

Bonus Questions

Onsite Amazon Question asked in May, 2022

Question 3

You are given the root of a binary tree with 'n' nodes where each node in the tree has 'node.val' coins. There are 'n' coins in total throughout the whole tree. In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent. Return the minimum number of moves required to make every node have exactly one coin.

Example

    3
  /   \
 0     0

Input:

root = [3,0,0]

Output:

2

Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Question 4

Given a string 's', return the lexicographically smallest subsequence of 's' that contains all the distinct characters of 's' exactly once.

Example 1

Input:

s = 'bcabc'

Output:

'abc'

Example 2

Input:

s = 'cbacdcbc'

Output:

'acdb'

Question 5

Given two strings 's' and 't' of lengths 'm' and 'n' respectively, return the minimum window substring of 's' such that every character in 't' (including duplicates) is included in the window. If there is no such substring, return the empty string ' '''' '.

Example

Input:

s = 'ADOBECODEBANC', t = 'ABC'

Output:

'BANC'

Explanation: The minimum window substring 'BANC' includes 'A', 'B', and 'C' from string t.

7 months ago

Akshay Sharma 990

Chandigarh

QUESTION 3

Solution

• Let's try to understand the approach using the diagram below:

  

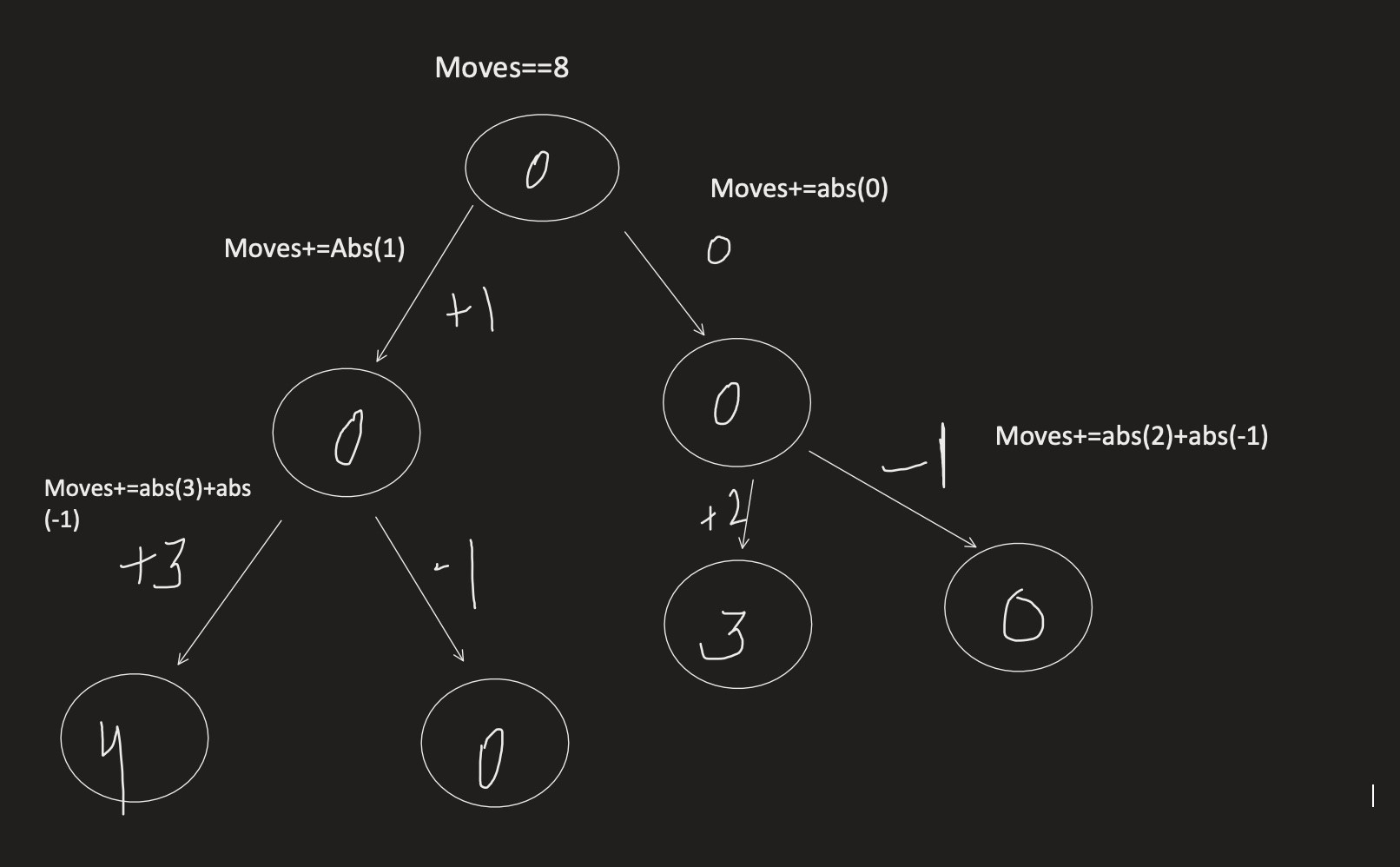
• We traverse the child first (post-order traversal), and return the balance of coins. For example, if we get '+3' from the left child, that means that the left subtree has 3 extra coins to move out. If we get '-1' from the right child, we need to move 1 coin in.

• So, we increase the number of moves by 4 (3 moves out left + 1 move in right). We then return the final balance: r->val (coins in the root) + 3 (left) + (-1) (right) - 1 (keep one coin for the root).

Pseudo code `

    int ans=0;
    int recr(TreeNode *root)
    {
    if(!root) return 0;
    int left = recr(root->left);
    int right = recr(root->right);
    int curr = root->val + left + right;
    ans += abs(curr-1);
    return curr-1;
      }`

20 months ago

Yash Sahijwani 940

Solution for Question 1

Analysis

In the question, we are given a string followed by queries of two types - one for updating the string, and the other for finding the score in a given interval. The score has been defined as the XOR of the frequencies of each distinct character in the interval [l, r]. Since the number of queries in 10^5, we need an efficient method which works in O(logn) or O(1) for each query, to update the string as well calculate the new frequencies.

A basic method can be to create a prefix array for each letter from 'a' to 'z', where pref1[i] stores the total number of occurrences of the letter 'a' that come before or at the index i, and similarly for all the other letters. Calculating number of occurrences will take O(1) time, by simply calculating pref1[r] - pref1[l-1]. However, updating the prefix array can take O(n) time.

A better method to do this is using Fenwick Tree. In Fenwick tree we can update the array in O(logn) time, and the prefix sums can also be calculated in O(1) time. You can view this link for a better understanding of Fenwick Tree. In this problem, if we want to update the array, for the letter we want to remove, we update that letter's array by subtracting 1 from the position we want to update (and hence all positions such that g(j) <= i <= j, using the fenwick update method), and to add a letter, we just add 1 in the same manner.

Fenwick Tree Implementation

void add_fenwick(int idx, int i, vector < vector < int > > &fenwick, int val)
{       
     int n = fenwick[0].size();
    while(i < n)
    {
         fenwick[idx][i] += val;
         i = i | (i+1);
    }
    return;
}
int calc_sum(int idx, int i, vector < vector < int > > &fenwick_tree)
{
  int ans = 0;
  while(i > 0)
  {
     ans += fenwick_tree[idx][i];
     i = (i & (i+1)) - 1;
  }
  return ans;
}
// Here idx refers to the character we want to update
// i refers to the position
// In calculate sum function I have kept terminating condition as i > 0, since I am using 1 based indexing

7 months ago

Akshay Sharma 990

Chandigarh

Question 4

Overview

• We are given a string s we need to find the lexicographically smallest string possible that has all distinct characters.
  • Mean the string we are going to print is the smallest possible for each s[i] and no two characters repeat in that string.

Solution

• We will be going to maintain a hashmap or frequency array and start traversing the string.
  • one we get to any position we are going to check if that character is already present in the frequency array or not.
  • If the character is already present we can skip it else we will mark it true in the frequency array.
  • Once we reach to end we start traversing the frequency array and check if freq[i] is not false so that we can print that character at once.
  • Time complexity : O(N)

7 months ago

Akshay Sharma 990

Chandigarh

Question 5

Overview

• We are given strings S and T.
  • We need to find a string such that every character in string T is included in string S (Including duplicates)
  • Let's assume the size of strings S and T would be less than 10^4.
  • Also complete string S could be the answer for our given solution.
  • There can be multiple solutions to this question but we need to return that substring which has minimum length among all.
  • if string T did not exist in string S we need to return empty string.

Solution

• Here we’re storing all the characters from string t to an unordered_map mp or use hashing.
• We are taking 3 variables, ans(to store the size of the minimum substring), start(to store the start index) & count(to store the map size, if it became 0 that means we got a substring)
• Now taking 2 pointers i & j, we’ll iterate using j & will decrement the element count in the map in c++ or hash map in java.
• if at any point the value became 0 that means we got all the elements of that char till now, so we’ll decrement the size of the count.
• In this way, we will decrement and once the count will be 0 if there is a substring with all the elements present.
• Now we’ll increment i and check if there is possible to remove any more characters and get smaller substrings.
• We’ll store the smaller length to ans & store the ith index in the start variable. Also, we’ll add the element to our map and increment the count variable if it became greater than 0.
• Now if the ans have some length except int_max, then return the substring from the start index to the length of ans. Else return the empty string.
• Time complexity: O(m), where m is the length of string s.

24 months ago

Gurankit Pal Singh 160

Solution for Question 2

This problem can be solved by binary searching on the answer. Let n be the length of the string and x be the number of operations performed. Make a prefix sum frequency array freq[n][26] from x+1 to n. Now, frequency from L to R for a letter j can be calculated by freq[R][j] - freq[L-1][j] in O(1). If the frequency of each letter in each range is less than 2, then the string would be a good string. Perform the binary search on x, so, the time complexity is O(nlogn26), and space complexity is O(n*26).

Pseudo Code:

check(operations, str, arr, ranges)
    freq[n][26]
    for i from operations to n
        ++freq[arr[i]][str[arr[i]]]

    for i from 1 to n
        for j from 0 to 25
            freq[i][j] += freq[i-1][j]

    for i from 0 to ranges.size
        L = ranges[i][0], R = ranges[i][1]
        for j from 0 to 25
            if freq[R][j]-freq[L-1][j] > 1
                return false

    return true

goodString(str, arr, ranges)
    n=arr.size
    start = 0, end = n, mid, ans
    while start < = end
        mid = (start + end)/2
        if check(mid, str, ranges)
            ans = mid
            end = mid-1
        else
            start = mid+1

    return ans

3 months ago

compiler • 0

Prayagraj

Question 3:

sample Input:

3
0 1
1 2
3 0 0

sample output:

3

code:

#include<bits/stdc++.h>
using namespace std;
int ans = 0;
int f(vector<vector<int>>&tree,vector<int>&coins,int node,int p)
{
  int coin = coins[node];
  for(auto&ch:tree[node]){
    if(ch!=p){
      coin+=f(tree,coins,ch,node); 
    }
  }
  ans+=abs(coin-1);
  return coin-1;
}
int main()
{
  int n;
  cin>>n;
  vector<vector<int>>tree(n);
  for(int i=1;i<n;i++)
  {
    int a,b;
    cin>>a>>b;
    tree[a].push_back(b);
    tree[b].push_back(a);
  }
  vector<int>coins;
  for(int i=0;i<n;i++)
  {
    int c;
    cin>>c;
    coins.push_back(c);
  }
  ans = 0;
  f(tree,coins,0,-1);
  cout<<ans<<endl;
  return 0;
}

3 months ago

compiler • 0

Prayagraj

Question 4:

i may be wrong

for input s = ba

output should be = banot ab

#include<bits/stdc++.h>
using namespace std;

int main() {
    string s;
    cin >> s;
    int n = s.size();
    vector<int> hash(26, 0);
    for (int i = 0; i < n; i++) {
        hash[s[i] - 'a']++;
    }
    vector<bool> visi(26, 0);
    stack<char> st;
    for (int i = 0; i < n; i++) {
        if (visi[s[i] - 'a'] == 0) {
            while (!st.empty() && st.top() > s[i] && hash[st.top() - 'a'] > 0) {
                visi[st.top() - 'a'] = 0;
                st.pop();
            }
            st.push(s[i]);
            visi[s[i] - 'a'] = 1;
        }
        hash[s[i] - 'a']--;
    }
    string ans;
    while (!st.empty()) {
        ans.push_back(st.top());
        st.pop();
    }
    reverse(ans.begin(), ans.end());
    cout << ans << endl;
    return 0;
}

8 weeks ago

AYUSH KUMAR • 0

Kolkata

Q1, Solution: 

Intuition and Explanation

Problem Understanding

The task involves handling two types of queries on a string of lowercase Latin letters:
1. Query Type 1 (L R): Calculate the XOR of the frequencies of all distinct letters in the substring from index L to R.
2. Query Type 2 (X Y): Update the character at position X to the Yth letter in the English alphabet.

To efficiently manage these queries, the solution uses a 2D Fenwick Tree (also known as a Binary Indexed Tree, BIT). This data structure supports efficient range updates and point queries, which are necessary for the operations required by the problem.

Data Structures

1. 2D Fenwick Tree (`fmwick`):
   - `fmwick[i][j]` keeps track of the cumulative frequency of the `j`th character (where `j` corresponds to 'a' + j) from the g(i) position of string up to index `i`, where g(i) is obtained by removing the first set bit of i.
   - Here, `i` ranges from 1 to n (length of the string) and `j` ranges from 0 to 25 (for each letter from 'a' to 'z').

Functions

1. `update(idx, ch, n, fmwick, val)`:
   - This function updates the Fenwick Tree to reflect the change in frequency of character `ch` at position `idx`.
   - It adds `val` (which can be +1 or -1) to the frequency of the character `ch` at `idx` and all its relevant ancestors in the Fenwick Tree. Don't forget to update the original string every time.

Time Complexity

1. Initialization:
   - Building the initial Fenwick Tree: `O(n * log n)` because each `update` operation takes `O(log n)` time, and it is performed `n` times (once for each character).

2. Query Type 1 (L R):
   - For each of the 26 characters, two `find` operations are performed, each taking `O(log n)` time.
   - Total time: `O(26 * log n)`, which simplifies to `O(log n)`.

3. Query Type 2 (X Y):
   - Two `update` operations are performed, each taking `O(log n)` time.
   - Total time: `O(2 * log n)`, which simplifies to `O(log n)`.

Thus, the overall time complexity for each query is `O(log n)`, making the solution efficient for large input sizes.

CODE

#include <bits/stdc++.h>
using namespace std;

#define ll long long

void update(ll idx, char ch, ll n, vector<vector<ll>> &fmwick, ll val)
{
    while (idx <= n)
    {
        fmwick[idx][ch - 'a'] += val;
        idx += (idx & (-idx));
    }
}

ll find(ll idx, char ch, ll n, vector<vector<ll>> &fmwick)
{
    ll sum = 0;
    while (idx >= 1)
    {
        sum += fmwick[idx][ch - 'a'];
        idx -= (idx & (-idx));
    }
    return sum;
}

int main()
{
    string str;
    cin >> str;
    ll n = str.size();
    vector<vector<ll>> fmwick(n + 1, vector<ll>(26, 0));

    for (ll i = 0; i < n; i++)
    {
        update(i + 1, str[i], n, fmwick, 1);
        // cout << str[i] << " : " << fmwick[i + 1][str[i] - 'a'] << endl;
    }

    ll q;
    cin >> q;
    while (q--)
    {
        ll a, b, c;
        cin >> a >> b >> c;
        if (a == 1)
        {
            ll ans = 0;
            for (ll i = 0; i < 26; i++)
            {
                ans ^= (find(c, 'a' + i, n, fmwick) - find(b - 1, 'a' + i, n, fmwick));
            }
            cout << ans << endl;
        }
        else
        {
            char temp = 'a' + c - 1;
            // cout << str[b - 1] << " : " << fmwick[b][str[b - 1] - 'a'] << endl;
            // cout << (temp) << " : " << fmwick[b][temp - 'a'] << endl;
            update(b, str[b - 1], n, fmwick, -1);
            update(b, temp, n, fmwick, 1);
            // cout << str[b - 1] << " : " << fmwick[b][str[b - 1] - 'a'] << endl;
            // cout << (temp) << " : " << fmwick[b][temp - 'a'] << endl;
        }
    }
}

27 days ago

Dhushyanthan Kannan • 0

Guwahati

#include <iostream>

#include <vector>

#include <algorithm>

#include <cmath>

#include<climits>

#include <map>

#include <set>

#include <string>

#include <queue>

#include <stack>

#include <bitset>

#include <utility>

#include <limits>

#include <functional>

#include <numeric>

using namespace std;

#define ll long long

#define pb push_back

#define fr(i,n) for(ll i=0;i<n;i++)

#define YES cout<<"YES"<<endl

#define NO cout<<"NO"<<endl

#define vl vector<ll>

#define vll vector<vector<ll>>

#define min_heap priority_queue<ll,vector<ll>,greater<ll>>

#define min_heap_pair priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>>

vector<ll>dx = {1,0,-1,0};

vector<ll>dy = {0,1,0,-1};

vector<char>dir = {'D','R','U','L'};

ll mod = 1e9+7;

long long expo_power(long long a, long long b)

{

    long long result = 1;

    while (b) {

        if (b & 1)

            result = (result * a) % mod;

        a = (a * a) % mod;

        b >>= 1;

    }

    return result;

}

class DisjointSet{

    public:

    vl parent,size;

    DisjointSet(ll n){

        parent.resize(n+1);

        size.resize(n+1,1);

        fr(i,n+1){

            parent[i]=i;

        }

    }

    ll findPar(ll node){

        if(node == parent[node]){

            return node;

        }

        return parent[node] = findPar(parent[node]);

    }

    void unionBySize(ll u,ll v){

        ll ulp_u = findPar(u);

        ll ulp_v = findPar(v);

        if(ulp_v == ulp_u){

            return;

        }

        if(size[ulp_u]<size[ulp_v]){

            parent[ulp_u]=ulp_v;

            size[ulp_v]+=size[ulp_u];

        }

        else{

            parent[ulp_v]=ulp_u;

            size[ulp_u]+=size[ulp_v];

        }

    }

};

vll segment;

void construct_tree(ll l, ll r, ll pos,string&s){

    if(l==r){

        segment[pos][s[l]-'a']++;

        return;

    }

    ll m = (l+r)/2;

    construct_tree(l,m,2*pos+1,s);

    construct_tree(m+1,r,2*pos+2,s);

    fr(i,26){

        segment[pos][i]=segment[2*pos+1][i]+segment[2*pos+2][i];

    }

}

void bring(ll l, ll r, ll pos, ll ql, ll qr, vl&use){

    if(l>qr || r<ql){

        return;

    }

    if(l>=ql && r<=qr){

        fr(i,26){

            use[i]+=segment[pos][i];

        }

        return;

    }

    ll m = (l+r)/2;

    bring(l,m,2*pos+1,ql,qr,use);

    bring(m+1,r,2*pos+2,ql,qr,use);

}

void update(ll l, ll r, ll pos, ll ql, ll qr,ll curr, ll val){

    if(l>r) return;

    if(l==r && l==ql){

        segment[pos][curr]--;

        segment[pos][val]++;

        return;

    }

    ll m = (l+r)/2;

    if(ql<=m){

        update(l,m,2*pos+1,ql,qr,curr,val);

    }

    else{

        update(m+1,r,2*pos+2,ql,qr,curr,val);

    }

    fr(i,26){

        segment[pos][i]=segment[2*pos+1][i]+segment[2*pos+2][i];

    }

}

int main(){

    ll t;

    cin>>t;

    while(t--){

        string s;

        cin>>s;

        ll n = s.size();

        ll q;

        cin>>q;

        segment.resize(4*n,vl(26,0));

        construct_tree(0,n-1,0,s);

        while(q--){

            ll a;

            cin>>a;

            if(a==1){

                ll ql,qr;

                cin>>ql>>qr;

                ql--;

                qr--;

                vl use(26,0);

                bring(0,n-1,0,ql,qr,use);

                vl curr;

                fr(i,26){

                    if(use[i]>0){

                        curr.pb(use[i]);

                    }

                }

                ll ans = 0;

                for(ll i=0;i<curr.size();i++){

                    ans = ans^curr[i];

                }

                cout<<ans<<" ";

            }

            else{

                ll ql,qr,val;

                cin>>ql;

                ql--;

                qr=ql;

                cin>>val;

                val--;

                ll curr = s[ql]-'a';

                update(0,n-1,0,ql,qr,curr,val);

            }

        }

    }

}