11 weeks ago

John 910

Hyderabad

Question 1

You are standing at the start of a very long road straight ahead. On the road, there are n cupcakes present. You are given the distance of each cupcake from the start of the road. Each of these distances is an integer, and multiple cupcakes can be present at the same distance from the start of the road.

You have to select 2 intervals of lengths k on the road and collect all the cupcakes that lie inside either of the intervals. The intervals are allowed to intersect. For example, for k = 3, the interval [1, 4] is a valid interval of length 3, and by choosing that interval, you can collect all the cupcakes that lie at a distance of 1, 2, 3 or 4 from the start of the road.

Find the maximum number of cupcakes that you can collect by picking 2 intervals as described as above.

Sample test case

n = 6
k = 1
distance = [1, 1, 2, 6, 8, 9]
expected output = 5

Explanation

We can pick the 2 intervals [1, 2] and [8, 9]. Both these intervals have length of 1 and there are a total of 5 cupcakes that lie in these intervals

• [execution time limit] 3 seconds (java)

• [input] integer n

  The number of cupcakes.

  1 <= n <= 2 x (10^5)

• [input] integer k

  The length of the intervals that you can pick.

  1 <= k <= 10^9

• [input] array.integer distance

  Array of n integers. The i th integer describes the distance of the i th cupcake from the start of the road.

  1 <= Ai <= 10^9, where Ai s are NOT NECESSARILY DISTINCT.

• [output] integer

  The maximum number of cupcakes you can collect.

Question 2

Given 3 positive integers K, L ,N where K <= L <= N

An integer set T of size L is called good if all integers in T are distinct and lie in range [1, N]

Let S be the set of all such possible sets T of given length L.

Let A be the uniformly and randomly chosen set from S. J(A) be the Kth smallest integer in this set A. Find sum of J(A) modulo 998244353 over all such good sets A.

Solve this for Q such query.

Input is given in form of 3 arrays Ks, Ls, Ns each size of Q.

ith query consists of K = ks[i], L = ls[i], N = ns[i].

Constraints:

1 <= Q <= 10^3

1 <= K <= L <= N <= 10^6

Sample Input:

ks: [2, 1, 2, 3]
ls: [2, 1, 2, 3]
ns: [3, 1, 2, 3]

Output:

[5, 1, 2, 3]

Question 3

Transactions

There is a bank and multiple transactions are queued throughout the day in format

Ram : Sham 500

Sham : Priya 600

Sham : Ram 200

There is a clearing house which settle these transactions a day later. Find the final transactions which clearing house should make.

Ram : Sham 300

Sham : Priya 600

Bonus Uber Onsite Question

Question 4

The maximum sum of 2 elements in a 2D integer matrix. Such that the 2 elements should not be in the same column or row.

22 months ago

Yash Sahijwani 940

Solution for Question 4

Analysis

In the question, it is mentioned that we need to find the maximum sum of two integers in the given matrix such that the two integers are neither in the same row or same column. So, if we iterate through all the elements of the matrix 1 by 1, we need to check what is the maximum value not present in the same row or column as the current element. So if we remove all elements from the same row and same column then we get something as shown below:

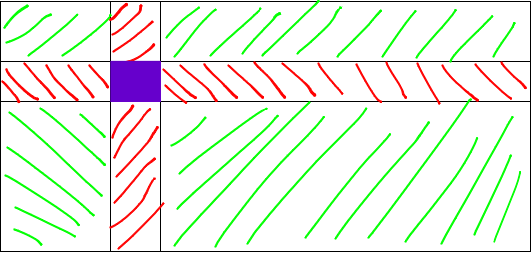
Here the purple box is the current element we are at, and the red row and column signify all the elements that we can't consider for this particular element. So we need to take the maximum element from the green regions which are formed in the image. There are 4 such regions, on the top left, top right, bottom left, bottom right.

Now to get the maximum from each of these regions we can use Dynamic Programming. For example, if we were to find the maximum values from the top left corner (0, 0) to the point (i, j) where i is the row and j is the column, then dp[i][j] = max(dp[i-1][j], dp[i][j-1], a[i][j]) where a is the initial matrix. So it basically checks the maximum elements of the smaller subrectangles formed and compares them with a[i][j]. In the figure below, the 2 subrectangles are marked.

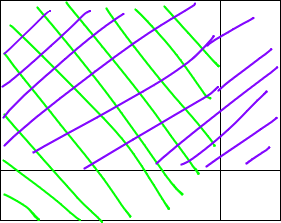
Similarly, we can do 4 types where the 1st type is dp[i][j] from top left, 2nd type is dp[i][j] from top right, 3rd is dp[i][j] from bottom left and 4th is dp[i][j] from bottom right. Then at i, j we can take max of the 4 regions.

So calculating the dp vectors will take O(nm) time and iterating through all elements will also take O(nm) time complexity. So the overall time complexity will be O(n*m).

Implementation

vector < vector < vector < ll > > > dp(4, vector < vector < ll > > (n+2, vector < ll > (m+2, 0)));
//top left
for(int i=1;i < = n;i++)
{
    for(int j=1;j < = m;j++)
    {
        dp[0][i][j] = max(dp[0][i-1][j], dp[0][i][j-1]);
        dp[0][i][j] = max(dp[0][i][j], a[i][j]);
    }
}
//top right
for(int i=1;i < = n;i++)
{
    for(int j=m;j > = 1;j--)
    {
        dp[1][i][j] = max(dp[1][i-1][j], dp[1][i][j+1]);
        dp[1][i][j] = max(dp[1][i][j], a[i][j]);
    }
}
//bottom left
for(int i=n;i > = 1;i--)
{
    for(int j=1;j < = m;j++)
    {
        dp[2][i][j] = max(dp[2][i+1][j], dp[2][i][j-1]);
        dp[2][i][j] = max(dp[2][i][j], a[i][j]);
    }
}
//bottom right
for(int i=n;i > = 1;i--)
{
    for(int j=1;j < = m ;j++)
    {
        dp[3][i][j] = max(dp[3][i+1][j], dp[3][i][j+1]);
        dp[3][i][j] = max(dp[3][i][j], a[i][j]);
    }
}
ll ans = 0;
for(int i=1;i < = n;i++)
{
    for(int j=1;j < = m;j++)
    {
        int val1 = max(dp[0][i-1][j-1], dp[1][i-1][j+1]);
        int val2 = max(dp[2][i+1][j-1], dp[3][i+1][j+1]);
        int val = max(val1, val2);
        ans = max(ans, a[i][j]+val);
    }
}

4 months ago

Ujjwal Srivastava 320

Bengaluru

Question 1

Overview

• n cupcakes are present on a road whose distances range from 1 to 10^9.
• Each of these distances is an integer and multiple cupcakes can be present at the same distance.
• We have to select two intervals of length k on road and collect all the cupcakes that lie in either of the intervals. These intervals are allowed to intersect.
• The final goal is to maximize the number of cupcakes collected.

Solution

• Firstly sort the given array/vector in increasing order.
• We will iterate from the last element of this array and keep another array smax.
• smax[i] will be the maximum number of cupcakes that can be collected by taking one interval of length k, if we considered elements from i, i+1.., n-1.
• Now for current element we will binary search for the largest index at which (a[idx_achieved]-a[current_idx]<=k). Lets say the index is idx_achieved.

• If we consider that the first interval starts from the current element the answer is:

          ans = max(ans, idx_achieved-current_idx+1+smax[idx_achieved+1])        
  

  where idx_achived-current_idx+1 = number of cupcakes in the first interval,

  and smax[idx_achived+1] = It is the same as 3rd point explained in the Solution part.

• While selecting an interval we do not worry if the length of the interval is less than k because we can extend it the right and achieve an interval of length k.

Code

    ll n, k;
    cin >> n >> k;
    vector<ll> a(n), smax(n + 1);
    for (ll i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    sort(all(a));
    smax[n] = 0;
    ll ans = 0;
    for (ll i = n - 1; i >= 0; i--)
    {
        ll lw = i, hi = n - 1;
        while (lw <= hi)
        {
            ll mid = (lw + hi) / 2;
            if (a[mid] - a[i] > k)
            {
                hi = mid - 1;
            }
            else
            {
                lw = mid + 1;
            }
        }
        ans = max(ans, hi - i + 1 + smax[hi + 1]);
        smax[i] = max(smax[i + 1], hi - i + 1);
    }
    cout << ans << endl;