9 weeks ago

xINFERNOx • 40

Delhi

Q1 ) Given a n*m matrix to find out no. of possible ways to reach n,m cell from 1,1 given some cells which shouldn't be visited in the grid. As a follow up, to find the indices of cells in the grid which occur in every possible path from the cell (1, 1) to (n, m) in the grid.

Q2) Given an array with n elements as persons, each person has i dollars where i is his index, You are also given 2 other arrays A[] and B[], where A[i] denotes the maximum number of poorer people alongside whom the i'th person can be happy, B[i] is the maximum no. of richer people alongside whom the ith person would be happy. To find the maximum number of people in the party to be invited where everyone is going to be happy.

8 months ago

Akshay Sharma 990

Chandigarh

Question 1

Overview

• The question statement is not well explained so let's discuss it here and make some assumptions also
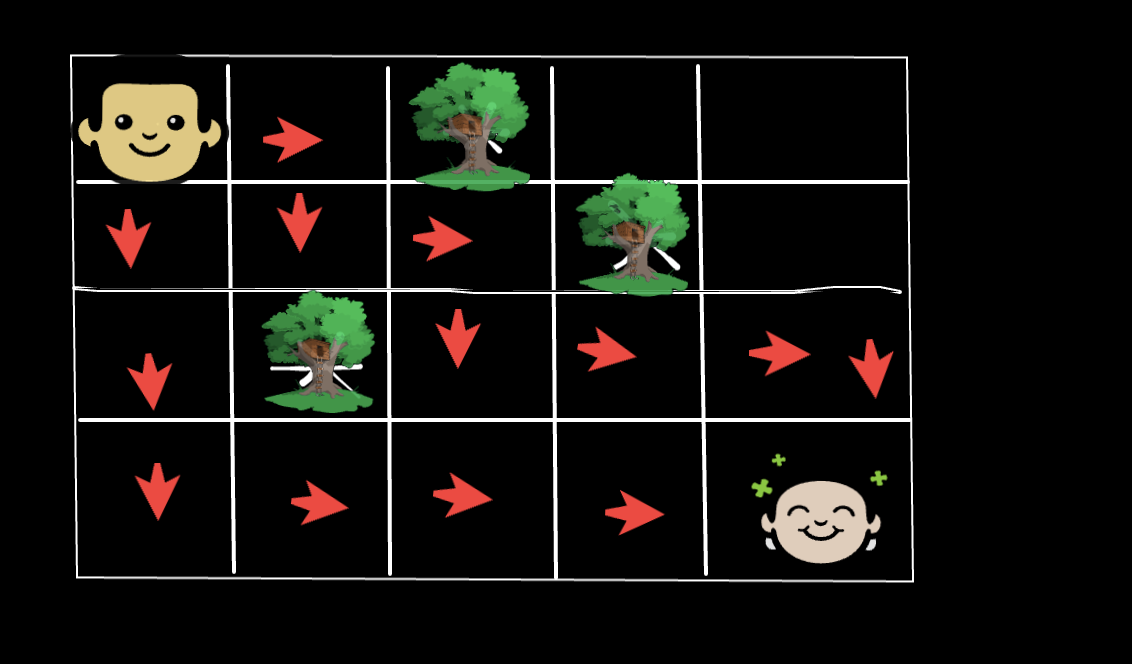
• We are given a matrix of size N*M we need to start from the cell (1,1) and reach the destination says (N, M).
• We need to print the total number of ways and also print the indexes of all such paths.
• Let's break the question to the first half only as the second half is nothing but making a recursive call to print all such indexes.
• The only move that is possible Go to the left or Down we are also given some blocked cells that cells we can't visit .

• The cell that is marked as 0 can be visitable and the Cell that is marked as 1 can't be visited.

  • The size of the Matrix that is N, M should always be less than 100.

  

Solution

• We can only move either down or right. Hence any cell in the first row can only be reached from the cell left to it, and any cell in the first column can only be reached from the cell above it.
• If any cell has an obstacle, we won't let that cell contribute to any path.
• We will be iterating the array from left to right and top-to-bottom. Thus, before reaching any cell we would have a number of ways of reaching the predecessor cells using DP we can easily find this.
• If the first cell i.e. Matrix[0,0] contains 1, this means there is an obstacle in the first cell. Hence we won't be able to make any move and we would return the number of ways as 0.
• Otherwise, if Matrix[0,0] has a 0 originally we set it to 1 and move ahead
• Iterate the first row. If a cell originally contains a 1, this means the current cell has an obstacle and shouldn't contribute to any path. Hence, set the value of that cell to 0. Otherwise, set it to the value of the previous cell i.e. Matrix[i,j] = Matrix[i,j-1] and do the same for the first column.
• Now, iterate through the array starting from cell Matrix[1,1]. If a cell originally doesn't contain any obstacle then the number of ways of reaching that cell would be the sum of the number of ways of reaching the cell above it and the number of ways of reaching the cell to the left of it. i.e Matrix[i,j] = Matrix[i-1,j] + Matrix[i,j-1]
• Below is the ways to reach the path starting from the top left cell.
• Time Complexity: O(M*N)

Pseudo-Code

 int m=a.size();
    int n=a[0].size();
    int ans=0;
    vector<vector<int>>dp(m+1,vector<int>(n+1,0));
    dp[0][1]=1;
    for(int i = 1 ; i <= m ; ++i)
        for(int j = 1 ; j <= n ; ++j)
            if(!a[i-1][j-1])
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
    return dp[m][n];

• For the printing indexes for all such paths we need to do the same recursive call but for that constraints are also quite less than the assumed constraints. We can easily do that by maintaining a pair of arrays or vectors in c++ and storing all the indexes recursively and printing them.

3 months ago

Ayush Gangwani 1.2k

New Delhi

Solution to Problem 2

Analysis

We can notice that if we can invite k people to the party, we can always invite k-1 people to the party by not inviting any one person from the selected persons as the remaining persons will still satisfy the conditions specified by the problem. Thus, we can solve the problem using Binary search on answer.

How to check if we can invite k persons to the party ?

Start selecting the persons from the richest to the poorest. Suppose that we have selected x persons so far and our only goal is to select k persons in total. Now we can select some person i if and only if A[i] >= x and B[i] >= k-x-1, i.e. if the i-th person can be happy with atleast x people richer than him and k-x-1 people poorer than him. Since we want to select as many persons as possible, it is always optimal to select such a person. Thus we can use this greedy strategy to choose the persons in a time complexity of O(N).

Now that we have a working predicate function for the problem, we can just binary search in the range [0,N] to solve the problem in a total time complexity of O(NlogN).

PseudoCode

solve(N, A, B):

    check(k):                                    //helper function that determines if we can choose k persons
        x = 0                                    //we have choosen x persons so far
        for i from N down to 1:                  //start choosing from the richest person
            if(a[i] >= x and b[i] >= k-x-1):     //we choose the ith person if it satisfies the conditions in the problem
                x++;
        return x >= k;                           //we return true if and only if we have choosen atleast k persons


    low = 0, high = N                            //binary search in the range [low,high] 
    while(hi > lo)
    {
        mid = low + (high - low)/2               
        if(check(mid)):                          //if we can choose k persons we reduce our search space to [mid,high]
            low = mid
        else:                                    //otherwise we reduce our search space to [low,mid-1]
            high = mid-1
    }
    return low                                   //finally low (=high) stores the maximum persons we can choose 

6 months ago

Raghav Gupta • 0

New Delhi

I'm getting wrong answer for test case 11. Not able to figure out what I'm doing wrong. Can you help?

#include<bits/stdc++.h>
using namespace std;

#define ll long long

int maxPath(vector<vector<int>> &mat, int i, int j, int m, int n, vector<vector<ll>> &dp)
{
    if(i < 0 || i>=m || j<0 || j>=n)
        return 0;
    
    if(mat[i][j] == 1)
        return 0;
    
    if(i == m-1 && j == n-1)
        return 1;
    
    if(dp[i][j] != -1)
        return dp[i][j];
    
    return dp[i][j] = maxPath(mat, i+1, j, m, n, dp) + maxPath(mat, i, j+1, m,n,dp);
    
    
}

int main()
{
    int m,n;
    cin>>m>>n;
    vector<vector<int>> mat(m, vector<int>(n));
    
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<n;j++)
            cin>>mat[i][j];
    }
    
    if(mat[0][0] == 1)
    {
        cout<<0; return 0;
    }
    
    vector<vector<ll>> dp(m+1, vector<ll> (n+1, -1));
    int ans = maxPath(mat, 0, 0, m, n, dp);
    
    cout<<ans;
    return 0;

}