Solution for Question 5 - Watchmen Trouble
Analysis
In the question, it is mentioned that we have N checkpoints on the left side of the river, and M checkpoints on the right side of the river, and there are P bridges which connect checkpoints on the left side to checkpoints on the right side. This means, that there is no bridge between checkpoints on the same side of the river. So, for each bridge, one endpoint is on the left side and one endpoint is on the right side.
We can visualize this using the following image: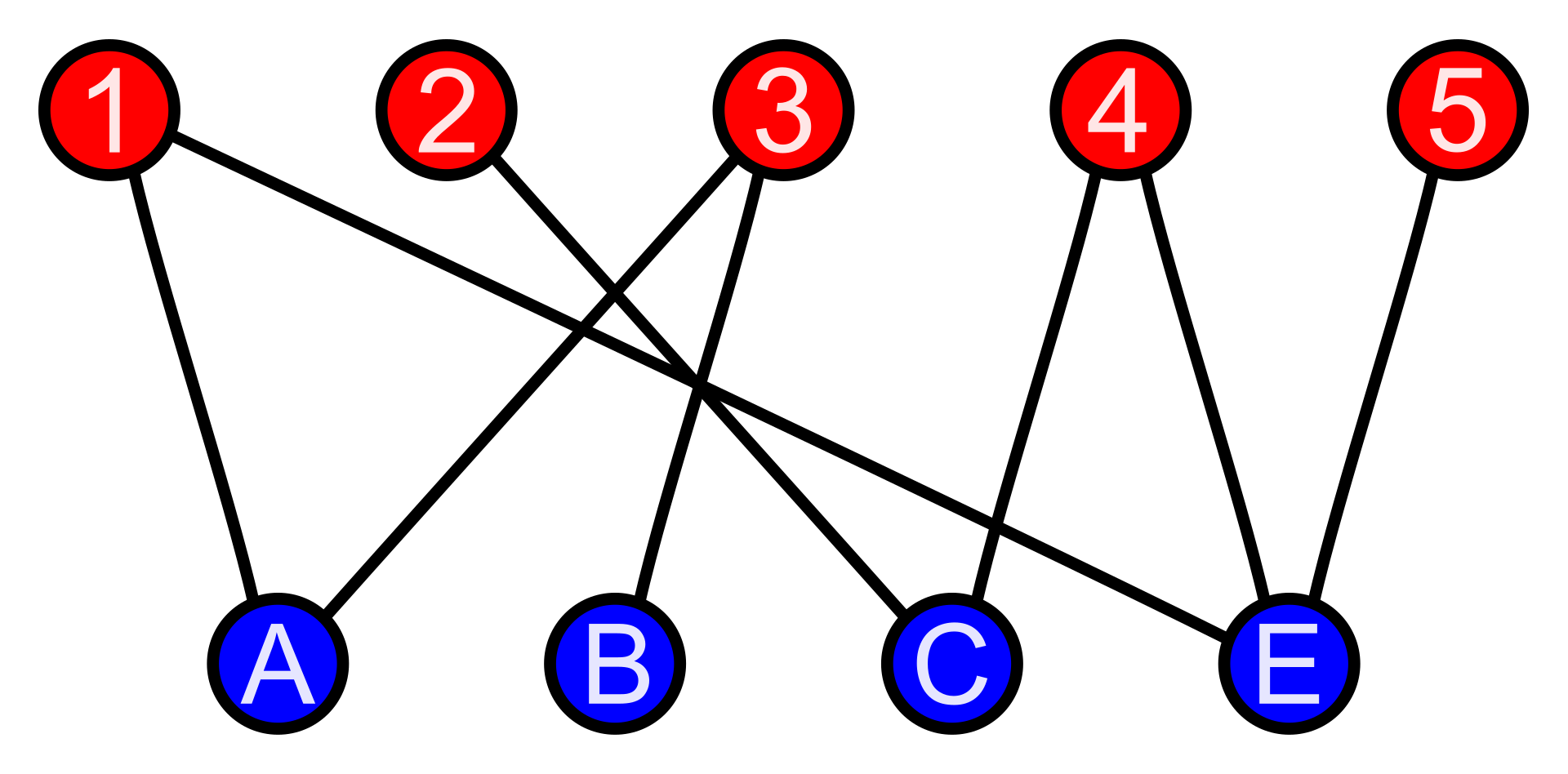
Here, the red vertices can be seen as checkpoints on the left side of the river, and blue vertices as the checkpoints on the right side of the river, and the edges are the bridges connecting them. From the image it is clear that the graph is a Bipartite Graph. A Bipartite graph is a graph in which we can separate all the vertices in the graph into 2 disjoint sets, say U and V, such that for each edge - one endpoint is in U and the other edge is in V. i.e. both endpoints of the edge can't be in the same set U/V. You can read more about Bipartite Graphs here.
Now, we need to find the minimum number of guards needed to protect all the bridges. A guard at a checkpoint can protect all bridges which have an endpoint at that checkpoint. So for all bridges, we need that atleast one endpoint of the bridge is covered by a guard. This becomes the minimum vertex cover problem. A vertex cover is basically a set of vertices which cover atleast one endpoint of each edge in the graph. The minimum vertex cover is a vertex cover with the minimum possible number of vertices. You can read more about minimum vertex cover here.
Here are some examples of a minimum vertex cover, where the red vertices are the vertices in the minimum vertex cover: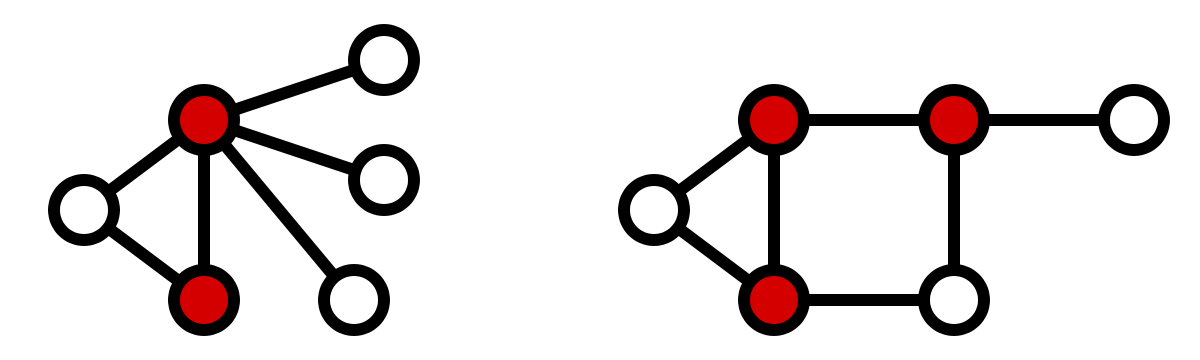
Now, calculating minimum vertex cover for a graph is NP-hard, but since it is a Bipartite Graph it can be done in polynomial time. To calculate the minimum vertex cover of a Bipartite Graph, we will use Konig's Theorem, which uses Maximum Bipartite Matching.
Hence, I'll give a brief explanation of what Matching in Graphs is, but it is advised to go through Matching, Maximum Bipartite Matching and Flows (since Maximum Bipartite Matching is calculated using Flows).
A matching in a graph is a set of edges, such that no 2 edges share a vertex. This means, that if there is an edge in a matching, then for both the endpoints of that edge, there cannot be another edge starting from those endpoints. A maximum matching is such that we cannot add any other edge to the matching (otherwise it will break the condition for it being a matching) and it has the maximum number of edges possible.
Now Konig's theorem states that in a Bipartite Graph, the size of the minimum vertex cover is equal to the size of the Maximum Bipartite Matching of the graph, i.e. the number of vertices in the minimum vertex cover is equal to the number of edges in the maximum bipartite matching. There are multiple proofs of the algorithm here but I'll try and explain the constructive proof here.
Proof for Konig's Theorem
Given a bipartite graph G(U, V, E), where U and V are the disjoint sets of vertices (red and blue) and E is the set of edges, we need to find a vertex set S⊆U∪V of minimum size that covers all edges, i.e. every edge (u,v) has at least one endpoint in S, that is u∈S or v∈S or both.
Let us consider the bipartite graph given below, where the edges in the maximum bipartite matching are marked in blue. The nodes in the upper row represent the vertex set U, and the nodes in the lower row represent the vertex set V.
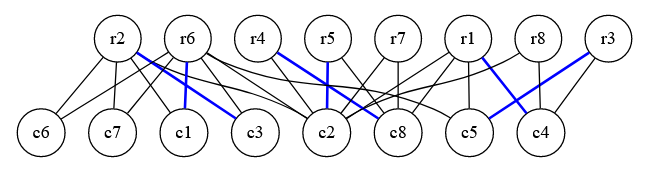
Now let us create a set Z which consists of all unmatched vertices in the vertex set U. By unmatched, I mean vertices which don't have a matching starting at them. From the image, we can see that r7 and r8 are the ones which will be in this set.
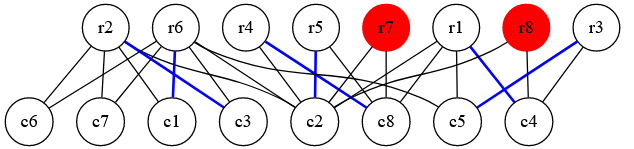
Then, to this set Z we add all vertices which are reachable using an alternating path from the vertices in Z. By alternating path, I mean a path in which the edges switch between edges in the matching and edges not in the matching (so for 2 adjacent edges, one should be in the matching and the other shouldn't). From this, we get the following (all vertices colored red are in the set Z)
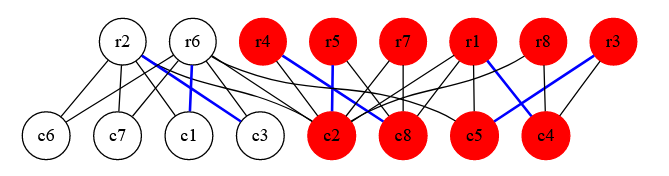
So, if we look carefully, since the initial nodes in the set were unmatched, they can reach the nodes in the set V using an edge not in the matching, then the nodes in the set V reach nodes in the set U using edges in the matching, and then again they use edges not in the matching and so on. So in an alternating path, we will have
(edge not in matching, edge in matching, edge not in matching, edge in matching, .... )
Now, if we have an edge (u, v) (where u is from the set U, and v is from the set V) in the matching, say M, then if v is in the set Z, then u will also be in the set Z. This is because, the alternating path would have reached v in which the last edge would have been an edge not in the matching. So that alternating path can be extended by using an edge in the matching. Hence, if (u, v) belong to the matching M, and if v belongs to Z, then u also belongs to Z.
Now, we consider the reverse case. If (u, v) belong to M, and u belongs to the set Z, then v also belongs to the set Z. This is because, initially u was not in the set, (since only unmatched vertices were in the set). So there must be an alternating path to get from those initial vertices to this vertex. To get to the vertex u, the last edge in the alternating path would have been an edge in the matching, and since edges in the matching can't share vertices, there is only one unique matching with vertex u as endpoint and that is (u, v), so to get to u, the alternating path must have gone through v.
From the above two conclusions, we come to the fact that for each edge in the matching M, either both the endpoints are in the set Z, or none of them are.
We define another set now, S = (U - Z) union (V intersection Z), This means that we take nodes from the set U, which are not in the set Z, and nodes from the set V, which are in the set Z. Hence, for each edge of the matching, if the matching is in Z, we take it's node v, and if the matching is not in Z, then we take it's node u. So each matching in the graph, has one endpoint in the set S, and so |S| = number of edges in the matching.
Now, Konig's theorem says that this set S is the minimum vertex cover. Let us consider an edge (u, v). If u is not in Z, then it is covered by S, since that vertex will be in the set S. Let us consider the case when u is in Z. If (u, v) is in the matching M, then as proved above, since u is in Z, v will also be in Z. If v is in Z, then it will also be in S, and hence the edge (u, v) will be covered. We are left with the case when (u, v) is such that (u, v) is not in the matching and u is in Z. If u is in Z, it must have been reached using an alternating path in which the last edge was an edge in the matching (or there was no edge at all - it was in Z at the start), Then we can always extend the alternating path using an edge not in the matching which is (u, v). So v will also be in Z, and hence (u, v) will be covered.
Hence, we have proved Konig's theorem and our solution will know consist of finding the maximum bipartite matching and then the size of that will be our answer.
Implementation
ll bfs(ll s, ll t, vector < ll > &parent, vector < vector < ll > > &adj, vector < vector < ll > > &capacity)
{
parent[s] = -2;
ll n = parent.size();
vector < bool > visited(n, false);
visited[s] = true;
queue < pair < ll,ll > > nodes;
nodes.push({s, LLONG_MAX});
while(!nodes.empty())
{
pair < ll,ll > node_flow = nodes.front();
ll node = node_flow.fi;
ll flow = node_flow.se;
nodes.pop();
for(ll i=0;i < (ll)adj[node].size();i++)
{
ll next = adj[node][i];
if(visited[next] || capacity[node][i]==0)
continue;
visited[next] = true;
parent[next] = node;
int new_flow = min(flow, capacity[node][i]);
if(next==t)
return new_flow;
nodes.push({next, new_flow});
}
}
ll flow = 0;
return flow;
}
ll maxflow(ll s, ll t, vector < vector < ll > > &adj, vector < vector < ll > > &capacity)
{
ll flow = 0;
ll n = adj.size();
vector < ll > parent(n, -1);
ll new_flow = 0;
while(new_flow=bfs(s, t, parent, adj, capacity))
{
flow += new_flow;
ll curr = t;
while(curr!=s)
{
ll prev = parent[curr];
ll idx = (find(adj[prev].begin(), adj[prev].end(), curr) - adj[prev].begin());
capacity[prev][idx] -= new_flow;
idx = (find(adj[curr].begin(), adj[curr].end(), prev) - adj[curr].begin());
capacity[curr][idx] += new_flow;
curr = prev;
}
}
return flow;
}
ll maximum_bipartite_matching(ll n, ll m, vector < vector < ll > > &edges)
{
ll total = n+m+2;
vector < vector < pair < ll,ll > > > temp(total+1);
vector < vector < ll > > adj(total+1);
vector < vector < ll > > capacity(total+1);
for(ll i=0;i < (ll)edges.size();i++)
{
ll u = edges[i][0];
ll v = edges[i][1];
v = v+n;
temp[u].pb({v, 1});
temp[v].pb({u, 0});
}
for(ll i=1;i < = n;i++)
{
ll source = n+m+1;
temp[source].pb({i, 1});
temp[i].pb({source, 0});
}
for(ll i=1;i < = m;i++)
{
ll sink = n+m+2;
temp[i+n].pb({sink, 1});
temp[sink].pb({i+n, 0});
}
for(ll i=1;i < = total;i++)
sort(temp[i].begin(), temp[i].end());
for(ll i=1;i < = total;i++)
{
for(ll j=0;j < (ll)temp[i].size();j++)
{
adj[i].pb(temp[i][j].fi);
capacity[i].pb(temp[i][j].se);
}
}
ll matchings = maxflow(n+m+1, n+m+2, adj, capacity);
return matchings;
}
void solve()
{
ll n,m;
cin > > n > > m;
ll p;
cin > > p;
vector < vector < ll > > edges;
for(ll i=0;i<p;i++)
{
ll u,v;
cin > > u > > v;
edges.pb({u, v});
}
ll ans = maximum_bipartite_matching(n, m, edges);
cout < < ans < < '\n';
return;
}

 Join Us
Join Us





isnt it violating note given in question that 1 character can map to only 1 other character?