5 weeks ago

Rohit • 600

Hyderabad

Question 1

Before the prayer assembly begins the students of different classes stand randomly in a single line. Often they become noisy. To maintain silence during the prayer assembly, the teacher tells them to stand in a particular sequence. The sequence is such that there are atleast N students of other classes standing between students of the same class.

Write an algorithm to output the final sequence in which the students will stand. If no such sequence is possible then output -1. If more than once sequence is possible, then output the lexicographically smallest string.

Input

The first line of the input consists of a string students, representing the initial sequence in which the students stand.

The second line consists of an integer count, representing the minimum number of students that stand between students of the same class.

Output

Print the string representing the final sequence in which at least d students of other classes stand between students of the same class. Print '-1' if it is possible. If more than one sequence is possible, then output the lexicographically smallest string.

Constraints

0 <= count <= 1000

Note: The class of students is alphanumeric character (i.e. [a-z][A-Z][0-9]).

Each character of the string students represents the class of the student.

Example

Input

ddgdghghh
2

Output

dghdghdgh

Explanation

students == ddgdghghh and count = 2

Different classes are = d, g and h

The final sequence = dghdghdgh

Question 2

Rose a music professor, decides to organize a group song competition in the Music Universe College. N number of departments will participate in the singing competition. Each department has M number of groups that want to participate. Rose decides the initial size of the groups in every department. The competition is organized in such a way that all the groups from the same department will sing on the stage together at the same time. Each department will sing in succession The music department has some mics that they will distribute to the groups and they will assign one mic to each group. In case they have surplus mics, they will regroup the students so that the number of students sharing each mic is minimized. After re-grouping Rose needs to find the number of students in the largest group from each department who are sharing a mic.

Write an algorithm to help Rose calculate the number of students in the largest group from each department who are sharing a mic after re-grouping.

Input

The first line of the input consists of three space separated integers - N, M and mic, representing the number of departments of the college, the number of groups from each department and the number of mics, respectively. The next N lines consists of M space-separated integers- g[0], g[1].....g[M-1] , representing the initial size of the group from each department.

Output

Print N space-separated integers representing the number of students in the largest groups from each department who are sharing a mic after re-grouping.

Note

The number of mics is more than or equal to the initial number of groups from each department.

Constraints

• 1 <= N <= 10^3
• 1 <= M <= 10^3
• 1 <= mic <= 10^6
• 1 <= g[0],g[1].......g[M-1] <= 10^9

Example

Input

2   5   7
10   8   6   4   3
12   10   8   4   5

Output

6   8

Question 3

There are N unique candies (labeled 1 through N) and K kids. You are asked to distribute all the candies to kids such that every kid has at most M candies. Return number of ways we can distribute candies.

There can be multiple ways to distribute the candies.

Example:

Input

N=3 K=2 M=2

Output

2

Explanation

(1st way) -> (1,2) and (2nd way)-> (2,1)

3 months ago

Ujjwal Srivastava 320

Bengaluru

Question 2

Overview

• N departments will participate in the singing competition. Each department has M groups that want to participate.
• The competition is organized in such a way that all the groups from the same department will sing on the stage together at the same time. Each department will sing in succession
• The music department has some mics that they will distribute to the groups and they will assign one mic to each group.
• In case they have surplus mics, they will regroup the students so that the number of students sharing each mic is minimized.
• After re-grouping Rose needs to find the number of students in the largest group from each department who are sharing a mic. -The number of mics is more than or equal to the initial number of groups from each department.

Solution

• For each department, we will do the following.

  • We will binary search on what can be the minimum possible size of the largest group.
  • Let's say currently we want to see if x can be the minimum possible size of the largest group.
  • Let's initialize a variable total_no_mics_required as 0.
  • Now we will iterate through all the groups in a department and if the size of a group is <= x then we will simply assign them 1 mic and increment total_no_mics_required by 1.
  • If the size of any group is > x, we have to count minimum number of mics that needs to be assigned such that size of each sub group is <=x. This will be simply (size_of_cur_group(g[i])-1)/x +1. We will increment total_no_mics_required by (size_of_cur_group(a[i])-1)/x +1
  • At the end we will see if total_no_mics_required is <= mic. If yes than size x of groups is possible else not.
  • In this way using Binary search we will find the suitable x for each group.

Code

ll n, m, mic;
cin >> n >> m >> mic;
vector<ll> ans;
for (ll i = 0; i < n; i++)
{
    vector<ll> g(m);
    ll mx = 0;
    for (ll j = 0; j < m; j++)
    {
        cin >> g[j];
        mx = max(mx, g[j]);
    }
    ll lw = 1, hi = mx;
    while (lw <= hi)
    {
        ll mid = (lw + hi) / 2;
        ll tot_no_mics_required = 0;
        for (ll j = 0; j < m; j++)
        {
            if (g[j] <= mid)
                tot_no_mics_required += 1;
            else
            {
                tot_no_mics_required += ((g[j] - 1) / mid) + 1;
            }
        }
        if (tot_no_mics_required <= mic)
        {
            hi = mid - 1;
        }
        else
        {
            lw = mid + 1;
        }
    }
    ans.pb(lw);
}
for (auto it : ans)
{
    cout << it << " ";
}
cout << endl;
return;

23 months ago

seettt • 0

has someone done Q1

20 months ago

hardik kapoor 130

Question 3

Disclaimer

Assuming the candles are not unique, as the example is given assuming that. If the candles are unique, we can solve it using recursion for small constraints.

Approach

This is just a case of distributing N identical balls into K non-identical boxes such that every box has almost M balls. This can be solved using generating functions, where we find the coefficient of x^N in (x^0+x^1+x^2+...x^M)^K.

After solving, this comes out to be

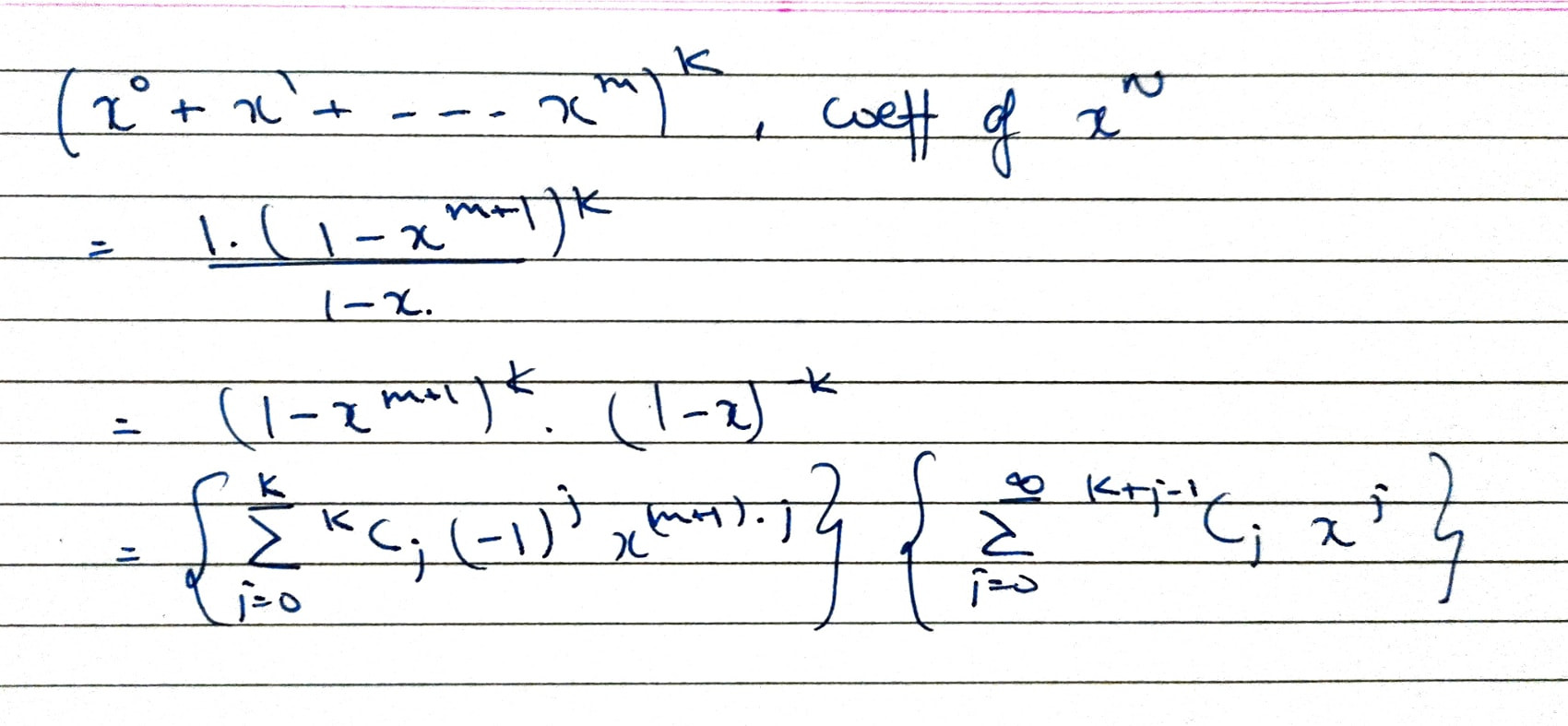
Hence, we can run a loop of K to find the coefficient of x^N in the solved expression.

C++ Code

vector<int> fac;

int ncr(int n,int r)
{
    int ans=fac[n];
    ans*=invmod(fac[n-r],mod);
    ans%=mod;
    ans*=invmod(fac[r],mod);
    ans%=mod;
    return ans;
}

int solve(int n,int k,int m)
{
    fac.assign(2e5+5,1);  // assuming maxk and maxn to be 1e5
    for(int i=1;i<2e5+5;i++)
        fac[i]=fac[i-1]*i,fac[i]%=mod;
    int ans=0;
    for(int i=0;i<=k;i++)
    {
        if(n-(m+1)*i<0)
            break;
        int c1=ncr(k,i);       // coeff of the first term
        if(i%2==1)
            c1=-c1,c1+=mod,c1%=mod;
        int i2=n-(m+1)*i;
        int c2=ncr(k+i2-1,i2);  // coeff of second term
        ans+=(c1*c2)%mod;
        ans%=mod;
    }
    return ans;
}

Complexity -> O(K * log (n)), log(n) factor for invmod calculation.

Take care of overflows

28 days ago

Akash 240

New Delhi

Question 1

Overview

• Given a string and a positive integer, rearrange characters of the given string such that the same characters become at-least d distance away from each other.

Approach

• The idea is to use extra space to store frequencies of all characters and maintain an array for inserting the values at the correct distance. Following is the complete algorithm:

• Let the given string be str and the size of the string be n, and the alphabet size is assumed as 256 (a constant).

• We scan input string str and store frequencies of all characters in an array freq.
• We create an array dist[] for inserting the values at the correct distance. dist[j] will store the least distance between the current position and the next position we can use the character ‘j’.
• If dist[j] <= 0, character ‘j’ can be inserted in the current position.

• Then run a loop n times

  1. Search for the next eligible character with maximum frequency and dist[j] <= 0.
  
  2. If we found such a character, we put that character at the next available position in the output array, decreased its frequency and reset its distance as d. If we don’t find any character, the string cannot be rearranged, and we return false.
  
  3. As we move forward in the output string, we decrement the distance of all characters in `dist[]` by `1.`
  

Complexity

Time Complexity: O(N), N is the size of string.