12 days ago

Gigaliths 460

IIT Ropar

Round 1 | 45 mins Technical + 15 mins (G&L)

Given Two time series

• The time series denote the spike that we have to make in discrete manner at that time.
• The value remains same for all time until the next updated spike.
• let T1 = [ (0,1) , (3,5) , (7,2) ] and T2 = [ (2,2) , (3,3) , (6,1) ]
• For T1 , value = 1 for [0,3) , value = 5 for [3,7) , value = 2 for [7,inf)
• For T2 , value = 0 for [0,2) , value = 2 for [2,3) , value = 3 for [3,6) and value = 1 for [6,inf)
• We have to return a new List which denotes T1 + T2
• T1 + T2 = [ (0,1) , (2,3) , (3,8) , (6,6) , (7,3) ]

Some good clarifications i asked :

• is time and value integer? ( No , can be double)
• is List sorted based on time? (Yes)
• Range of time and value? (Assume Infinite)

• Can there be 2 spikes for same time? (No , time wont be repeated)

• Inititally misunderstood the question , clarified the question again. (wasted 10mins)

• Was able to explain and code up a O(N) solution using two pointers.

Follow up questions

• Lets say we have M such time series , how should we approach?
• Came up with divide and conquer strategy to split M->M/2->M/4 ....2 and merge them bottom up using code to merge T1+T2.
• Time Complexity - O(Log(M)*N) , space = O(Log(M)) (recursion stack)

Round 2 , 45mins technical

Implement a Cache management class.

class Cache{
    Cache(int capacity){};

    int get(int key);

    int put(int key , int value);
}

Has fixed capacity and Remove the oldest inserted key if there is size overflow.

Some good clarifications i asked :

• will key be integer ? (Yes)
• do we need to handle cases for invalid requests? (example capacity <= 0) ? (Yes)
• will value be integer? (Yes)

Follow Up questions

• Implement LRU cache.

Pretty much finished this round in 25mins and had good amount of chat regarding the work i did during my summer internship.

Round 3 , 45mins technical + 15mins G&L

Initial Problem : Easy version

Follow Up : Hard Version

Under Progress

Question

Modifiy the input string with following substitutions.

S = "Alice saw a tiger"
subs = [(0,5,"Bob") , (13,18,"cat")]  {L,R,string}
result = "Bob saw a cat"

Some good clarifications i asked :

• is subs List sorted? (No);
• Are all characters english alphabets? (Yes);
• Are the ranges disjoint? (Yes , for now :) )

Approach for initial problem

• Came up with a binary search solution ,
• sort the subs List based on L
• scan through S from left to right and search for match in subs.
• Replace if there is a match , else append current character and keep scanning.

Follow up

• The ranges are not disjoint now. ( we should replace with the string of an overlapping range that comes first in subs)
• subs = [ (4,6,"hi") , (1,2,"bye") , (2,5,"ohho") , (6,6,"hehe")];
• The range 4,6 overlaps 2,5 which overlaps 1,2 , Hence 1,2 indirectly overlaps 4,6.
• Now when we reach index 1 in S , we will replace it with "hi" and jump to R = 6.
• since range (4,6) is the first range in subs that indirectly overlaps with (1,2).

Approach for follow up

• Came up with a Disjoint set Union solution.
• Merge those ranges that overlap with each other.
• Do Union by Size and store the [min_index , minL , maxR] for each component.
• Make a new merged_subs = [ (minL , maxR , subs[min_index])] for each DSU component.
• Now the question is same as first question , modifying string with disjoint ranges.

G&L (some i remember)

• What would you do if your team lacks innovation
• What if your manager isnt being helpful
• What if one of your team mates arent speaking up
• What if your team is not able to figure out on how to implement something.
• How to bring up innovations ```

12 days ago

Gigaliths 460

IIT Ropar

Question 1 : Solution

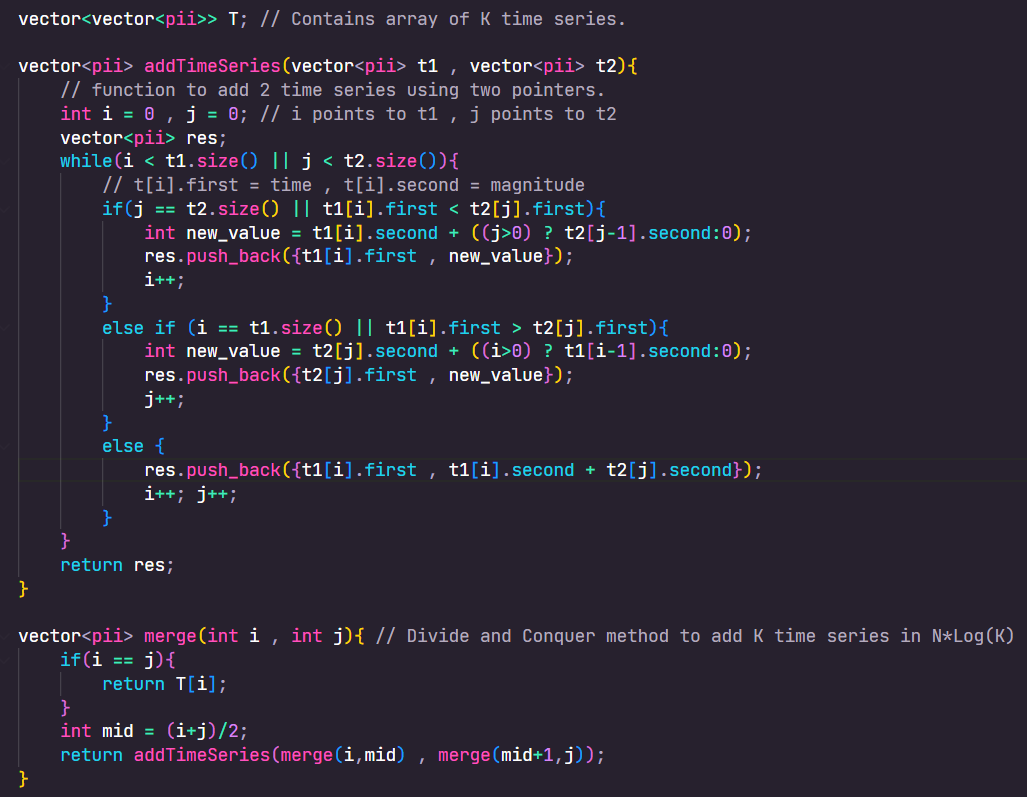
Adding 2 Time Series Data

• First part of the problem is to figure out how to add 2 time series data.
• Looking on few test cases will help you understand how the summation works and will help you come up with a two-pointer method.
• The main idea is to append the value to the result whose time is lesser and the magnitude of this point will depend on the magnitude of previously added point.
• There are few edge cases you might need to handle , but the below code will give you a good idea on the implementation.

Adding K Time Series Data

• We know how to add two time series data , and adding the K time series in any order should produce the same result.
• We can use a Divide and Conquer approach to add them.
• Let Merge( i , j ) = result of adding all time series data from T[i ..... j]
• Merge(0 , K) -> Merge(0,K/2) + Merge(K/2+1 , K)
• Base Case = Merge( i , i ) = return T[i]

Complexity

• O(N) to add two time series.
• O(NLog(K)) to add K time series of average length N.

Code