9 weeks ago

John 910

Hyderabad

Question 1

Traveler Fund

A traveler is traveling form city of zeta to omega. He starts with X amount of money. Every day he spends some money and also he may work on some days to earn money. He may find good work some day and end up earning more than what he spends that day. It also may happen that he spends more than what he earns on any day. You are given an array of integers which represents his net savings (earning -expense) on any day. You need to find out minimum amount the traveler should begin with to ensure that he always have some money (>0) at the end of any day.

Constraints:

-200<=a; <=200 , where aj are array elements O<<=100, where i is the array length X>=0

For example:

Input:

3 //Array length 4 //Array elements start 2 -3

Output:

0

Explanation:

Traveler saves $4 on first day, $2 on second day and $-3 on third day (expense is more on 3 day than earnings). End of the first day, he has X + $4 End of the Second day, he has X + $(4+2) End of third day, he has X + $(4+2-3)

Question 2

Jewellery Designer

Natalie is a famous jewellery designer, known for her pearl necklace designs. She has a team that helps her create unique designs made of different types of pearls. The team creates individual string of pearls, and Natalie then arranges the strings in a beautiful way to make necklace. To begin with, Natalie prepares a rough sketch of the necklace by using a single character code to represent every pearl type she uses. The necklace design therefore looks like a series of strings in N different lines. Natalie's secret to making beautiful design to follow one specific rule. The rule is that two pearl strings can be consecutively arranged only if the two strings have a similar suffix chain such that length of the similar suffix chain is atmost one less than the length of the longer string i.e. two strings A and B are consecutively arranged only if LSC(A,B) >= max(|A|,|B|)-1 , where |A| indicates the length of string A.

Example:

A: "gbpy"

B: "sbpy"

C:"bpy"

D:"bmy"

LSC(A,B)=max(|4|,|4|)-1=3

In this example atleast 3 suffix codes should exactly be same in A and B.

Her Team has brought in today's pearl strings, and Natalie is arranging them consecutively in necklace. She wants to create as big a necklace as possible. Write a program to help her arrange the longest possible sequence of strings, such that each two consecutive strings follow the rule.

Input:

4

gbpy

sbpy

bpy

bmy

Output:

3

Explanation:

Number of strings= 4

Consider first 2 strings "gbpy" and "sbpy", they have 3 similar pearls in the suffix chain "bpy" hence LSC=3 Max(|4|,|4|)-1=4-1=3 Hence these 2 strings can be consecutively arranged.

Similarly both "gbpy" and "sbpy" can be arranged with "bpy" also. However the string "bmy" does not have a suffix chain similar enough with any other string to follow the rule. Hence the longest possible arrangement is with 3 strings and the O/P is therefore 3.

Input 2:

5

rgb

ygb

mrwfna

gb

b

Output:

4

The longest possible arrangement is with 4 strings

rgb

ygb

gb

b

Question 3

Tiles Arrangement

Benita has a grid with N rows and three columns. Lisa has written an integer value (lesser than 10^6 by absolute value) in each cell of the grid. Benita has K tiles at her disposal, the tile dimensions being 2x1 cells. She has to arrange all of the tiles on the grid either horizontally or vertically, such that each tile covers exactly two cells of the grid. The tiles cannot overlap. Bonita wants to cover the largest sum of numbers possible with the tiles - write a program to help her.

Read the input from STDIN and print the output to STDOUT. Do not write arbitrary strings anywhere in the program, as these contribute to the standard output and test cases will fail.

Constraints:

1 <= N <=1000

1 <= K <=1000

Input Format:

The first line of input contains N, the number of rows and K, the number of tiles available. separated by a single whitespace. The following N lines contain three integers each, representing the values written in rows 1 to N of the grid.

Output Format:

Single line of output contains the maximum sum possible to be covered with exactly k tiles.

Sample Input 1:

5 3
2 1 -1
1 3 2
0 2 3 
2 1 1 
3 3 0

Sample Output 1:

16

Explanation:

It is optimal to place all tiles horizontally, along the right edge of the second row, right edge of the third row and along the left edge of the final row, which gives the maximum sum 16.

   2      1      -1
   1      3       2
   0      2       3
   2      1       1
   3      3       0

Sample Input 2:

2 2
0 4 1
3 5 1

Sample Output 2:

13

Explanation:

   0      4      1
   3      5      1    

18 months ago

Ayush Kumar Shaw 110

Solution to Question 3

This is a simple variation of the standard problem dp on profiles. So, we solve it using dynamic programming. We can keep a 3 variable state (i,j,k) which denotes the maximum sum that can be obtained by considering the first i rows and cells that form a bitmask k in the (i+1)th row by placing j cells. We can place one tile at a time and keep updating the dp table. Finally our answer will be dp(n,k,0). Note that dp(i,j,0) is the same state as dp(i-1,j,7). This solution works in O(n * k * 4^3). It can be optimized a bit to work in O(n * k * 3^3) by iterating only on the meaningful masks where transitioning is possible from a certain state.

Code Link

2.2 years ago

Dolton Fernandes 30

Solution to Problem 2:

Analysis

1) From the constraints, we can deduce that two consecutive strings will differ in length by at most 1.

2) Without loss of generality we can relax the constraint from LSC(A,B) >= max(|A|,|B|)-1 to "Suffix of length exactly max(|A|,|B|)-1 is equal"

3) The answer will always be in sorted order of length of the strings.

How to solve?

If we convert the input given to a suffix trie, then for each of the nodes (strings), we can easily find the answer for it (considering it to be the string with the largest length) using DP, and in the DP calculation, we just have to consider the nodes in the same level or in one level below. Let dp[s] be the answer if we take string 's' as the largest length string, then the final answer is nothing but max(dp[s]) ∀ s∈Input_Strings. dp[s] is nothing but the number of nodes with the same immediate parent + max(dp[s']) where s' is a child of s.

Note: DP calculation is only done on immediate children nodes because the length of strings shouldn't differ by more than 1.

Example

n=5, arr = ["rgb", "ygb", "mrwfna", "gb", "b"]

The suffix trie that will be formed is:

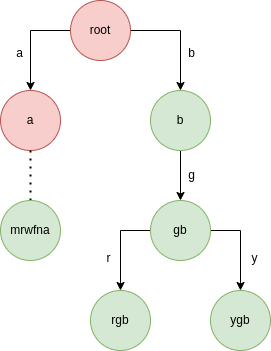
, where green nodes are the strings present in the input array.

After DP calculation, the values for nodes become as shown below:

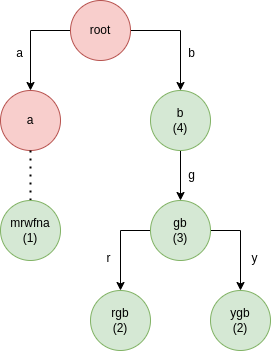
Final answer is max(dp[s]) = max(1, 4, 3, 2, 2) = 4

3 months ago

Ayush Gangwani 1.2k

New Delhi

Solution to Problem 1

Analysis

A common idea for solving such problems is to ask "Can we do the task with a given value of X". If we can answer this question optimally, then we can also solve the problem. The idea is to binary search for the value of X and finding out whether a given value of X would be sufficient. This technique is called Binary Search on Answer.

Implementation

The only important step is to find a predicate function for the problem. It turns out that for this problem, the predicate function is simply simulating the traveler's journey. Since we have a given starting value of X (thanks to the binary search), we can simply simulate the journey and check if the traveler's money becomes negative(or zero) at some point or not. If it does, this value of X is not sufficient. If it doesn't become negative(or zero) at any point of the traversal, this value of X is sufficient. We can update the limits of our binary search accordingly. The time complexity is thus O(NlogN) as the time complexity of the predicate function is O(N) and the time complexity of binary search is O(logN).

PseudoCode

check(savings,X):  
    for saving in savings:
        X += saving
        if(X <= 0):
            return false

    return true

travelerFund(savings):
    lo = 0, hi = inf, ans = 0
    while (hi >= lo):
        mid = (lo + hi)/2
        if(check(savings,mid)) ans = mid, hi = mid-1;
        else lo = mid+1 
    return ans

Remarks

There is also an O(N) solution to the problem using prefix sums. We can just calculate the prefix sum array of the given array.

The prefix sum value at some index i represents the amount of money left with the traveler at the end of day i, if he starts with 0 amount (initially X = 0). Thus to ensure that there is some amount of money left with the traveler at the end of any day, we only need to consider the minimum value of prefix sum array.

• If the minimum value is > 0, We can claim that the required minimum value of X is 0.
• If the minimum value is <=0, We can claim that the required minimum value of X is abs(minimum value)+1, so as to have exactly the minimum amount of money (1 unit) at the end of this day.