Avg CTC: 12lpa for Google interns
Job Role: STEP intern
STEP Intern: Student Training Engineering Program
Location: Bangalore, Hyderabad
Application Link: Click here to apply
Question 1
Special Paths




Question 2
Count Pairs




Solution to Problem 1
Analysis
Since all the nodes in a path between the starting node and the terminating node have to be smaller than or equal to them, we can add the nodes in increasing order of their value. More formally, we will maintain a DSU and add the nodes in increasing order of their values. Now when we add a node (and its respective edges), we join two disjoint components (by the properties of a tree, every edge joins two disjoint components) and since all the nodes so far were smaller than or equal to current node in the value, the number of paths spanning through this node is equal to the product of frequency of the value of current node in the two components. Thus we can keep adding the nodes in the increasing order of their values and keep adding the number of new special paths formed.
Suppose we have a tree like below.
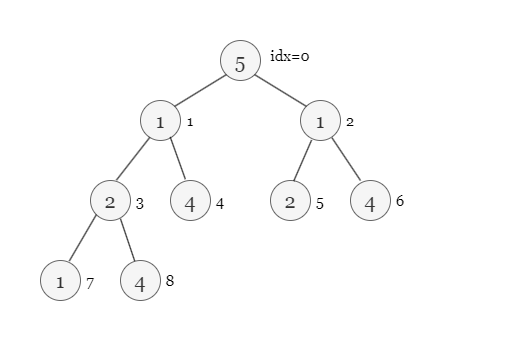
Start with value = 1, we have 3 separate roots 1, 2 and 3.
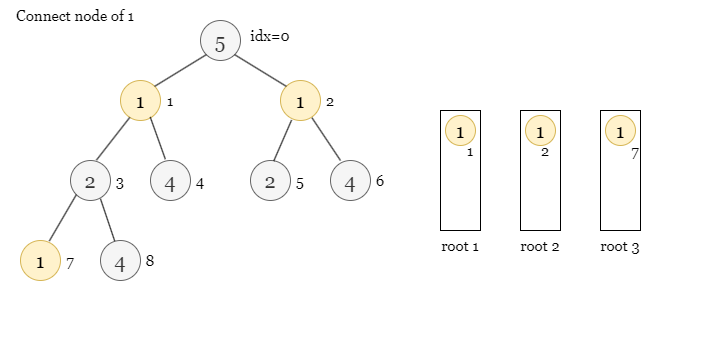
Now we move to values = 2, those two nodes connect to some neighbors with values = 1. Hence we get 1 special path from node 1 to 7 spanning through node 3
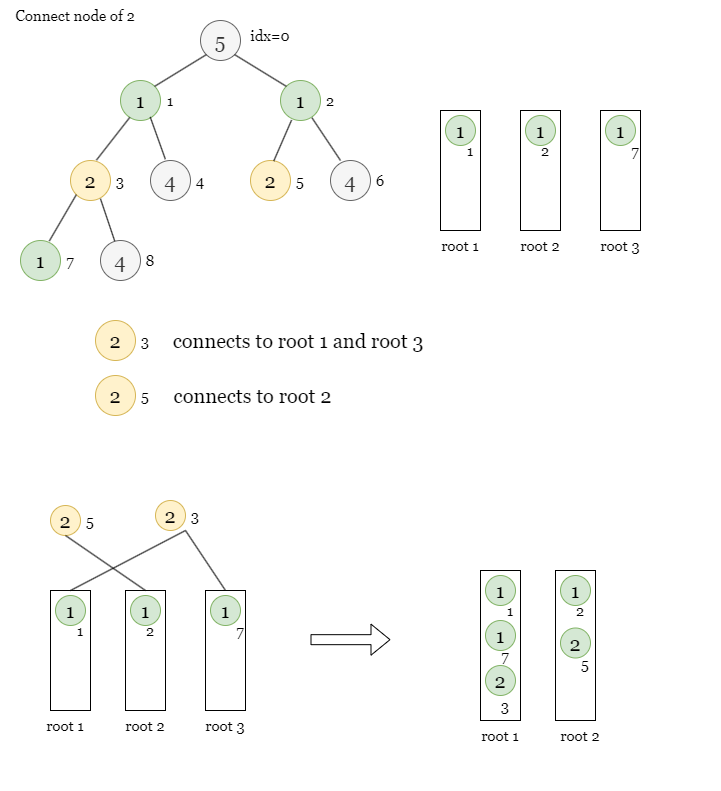
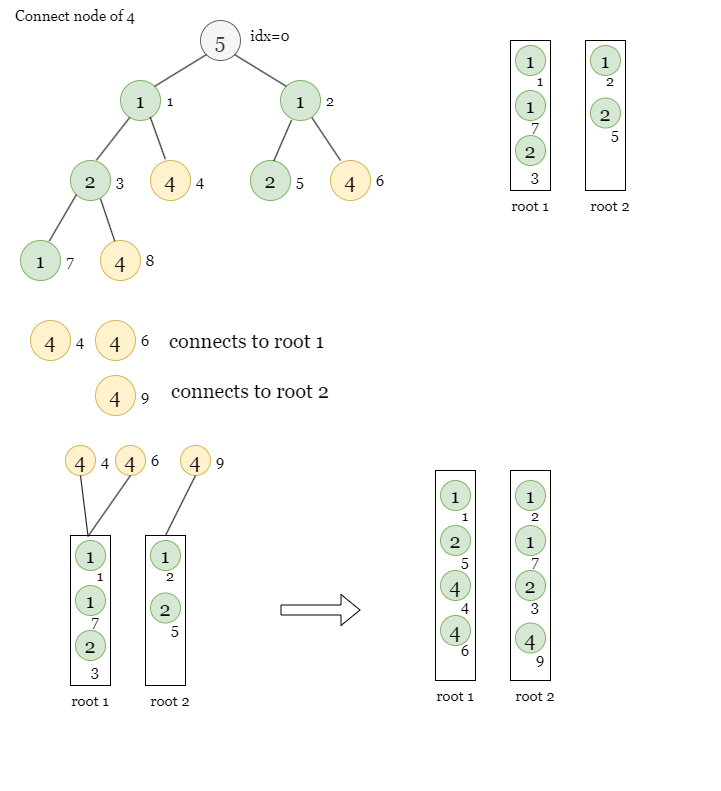
Now we move to value = 4. We create one more special path from node 4 to node 8.
C++ Code
int numberOfSpecialPaths(vector<int>& vals, vector<vector<int>>& edges)
{
int n = vals.size();
vector<int> o(n), adj[n], par(n), sizes(n,1);
map<int,int> freq[n];
for(int i=0; i<n; i++) o[i] = i, par[i] = i, freq[i][vals[i]] = 1;
sort(begin(o),end(o),[&](const int& l, const int& r){ return vals[l] < vals[r]; });
for(auto& edge:edges)
{
if(vals[edge[1]] > vals[edge[0]]) swap(edge[1],edge[0]);
adj[edge[0]].push_back(edge[1]);
}
int ans = 0;
function<int(int)> find = [&](int x)
{
return par[x] = (par[x] == x) ? x : find(par[x]);
};
auto merge = [&](int a, int b)
{
int temp = vals[a];
a = find(a);
b = find(b);
if(a == b) return ;
ans += freq[a][temp] * freq[b][temp];
if(sizes[b] > sizes[a]) swap(a,b);
sizes[a] += sizes[b];
par[b] = a;
if(freq[b].size() > freq[a].size()) swap(freq[a],freq[b]);
for(auto& [val,cnt]:freq[b]) freq[a][val] += cnt;
};
for(auto& node:o)
{
for(int child:adj[node]) merge(node,child);
}
return ans;
}
Solution to Problem 2
Analysis
We need to count pairs i,j (1 <= i < j <= n) satisfying the inequality ai - aj + c <= bi - bj + d. We can rearrange the terms to obtain ai - bi <= aj - bj + d-c. Thus for a given j we need to find number of i such that i < j and ai - bi <= aj - bj + d-c. We need to just query the number of elements smaller than some value discovered so far and keep adding the new elements. We can do this simply by iterating through the array elements and maintaining a Fenwick Tree (BIT)/Segment Tree/ C++ PBDS.
PseudoCode
solve(a, b, n, c, d):
ans = 0
ds = new ordered_set<int> //use either BIT/segment tree or PBDS
for j from 1 to n:
ans += ds.query_smaller_than_or_equal_to(a[j] - b[j] + d-c) //as explained just query values smaller than a[j]-b[j]+d-c in the container so far
ds.insert(a[j] - b[j]) //and add the value corresponding to the jth element
return ans

 Join Us
Join Us
If you are not using PBDS, then I think you have to use Coordinate Compression in order to use values as indexes as Array elements can go upto `1e9`. At least this is how I did it. Also I think deciding which values to compress is something to think about here. I will explain a bit.
So the values we are going to compress should be all the `A[i]` values and `A[i] + (c - d)` values, because these are the only values which will be compared against one another. So basically 2*N number of values. It's reasonable and works.
Since the official solution only has pseudo code, I will leave my solution with (Fenwick Tree + Coordinate Compression)