9 weeks ago

John 910

Hyderabad

Avg CTC: 14lpa

Job Role Description: Return to Work Program for Women on a Career Break-Software Engineer

Application Link: Software Engineer Role

Question 1

Given N boxes containing different number of Books in each box(numBook[i]), take a minimum number of books from the boxes conditions are such that:

• you must take either all or none of the books inside a given box.
• you cannot skip taking books from boxes adjacent to each other. Box1 and 2 can not be skipped but you can skip box 1 and 3.
• you cannot take books from boxes adjacent to each other. Box1 and 2 can not be taken but you can take box 1 and 3.
• you must have a minimum number of books in your hand

For Example

If there are 6 boxes and the number of books in box are {7,2,13,12,9,1} then the minimum number of books u can take is 15(by skipping box 1,3,5).

Constraints

• 0 > N > 100
• numBook[i] < 10000

Question 2

In the game of cricket, players can score runs by hitting the ball delivered at them(by another player called bowler) and running between designated spots(wickets).

Suppose if a player is only allowed to score 1,2,4 and 6 runs in a ball.How many ways the player can score N runs without hitting consecutive 4s?

For Example

To score 4 runs, the player can hit the runs in subsequent balls in the following ways:

1,1,1,1

1,1,2

1,2,1

2,1,1

2,2

4

Output:

6

21 months ago

Yash Sahijwani 940

Solution for Question 2

Analysis

In the question, it is mentioned that we need to find the total number of ways in which a player can score N runs without hitting consecutive 4's. The player can hit 1, 2, 4 or 6 runs in every ball. We can approach this problem using Dynamic Programming.

In Dynamic Programming we need to define an appropriate state to solve the problem. In this case we can define the state as (number of runs scored, was last ball a 4 or not). So our state consists of two things, the number of runs scored, and whether the last ball was a 4 or not.

So, we need to calculate dp[n][0] + dp[n][1]. That is the number of ways n runs can be scored such that the last ball was not a 4 + number of ways n runs can be scored such that last ball was 4.

Now, dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-2][0] + dp[i-2][1] + dp[i-6][0] + dp[i-6][1]

We have this transition, which means that if the last ball was not a 4, then the last ball was either a 1, 2 or 6. So we add dp[i-1], dp[i-2], dp[i-6]. Since, the last ball was 1, 2 or 6, the 2nd last ball can either be a 4 or not a 4. There is no restriction on the 2nd last ball, so we add both dp[i-1][0] + dp[i-1][1].

For, dp[i][1] = dp[i-4][0]

We have this transition because if the last ball was 4, then before the last ball the number of runs were i-4, and the 2nd last ball can't be a 4.

dp[0][0] = 1;
for(ll i=1;i < = n;i++)
{   
    //calculating dp[i][0]
    if(i-1 > = 0)
        dp[i][0] = (dp[i][0]%mod + (dp[i-1][0]%mod + dp[i-1][1]%mod)%mod)%mod;
    if(i-2 > = 0)
        dp[i][0] = (dp[i][0]%mod + (dp[i-2][0]%mod + dp[i-2][1]%mod)%mod)%mod;
    if(i-6 > = 0)
        dp[i][0] = (dp[i][0]%mod + (dp[i-6][0]%mod + dp[i-6][1]%mod)%mod)%mod;

    //calculating dp[i][1]
    if(i-4 > = 0)
        dp[i][1] = (dp[i][1]%mod + dp[i-4][0]%mod)%mod; 
}
ll ans = (dp[n][0] + dp[n][1])%mod;

8 months ago

Akshay Sharma 990

Chandigarh

Question 1

Overview

• We are given Boxes that contain some books inside them.
• We have to choose boxes optimally such that in the last we have the minimum number of books.
• Either we can choose a box or not choose but with the condition that we can't skip two adjacent boxes.

Approach

• The question is nothing but to find the minimum number of books.
• As we can't skip the two adjacent boxes so the answer is simple the sum of the minimum of adjacent elements starting from 1 to n-1 or 2 to n.
• Below is a diagram that will clear the approach:
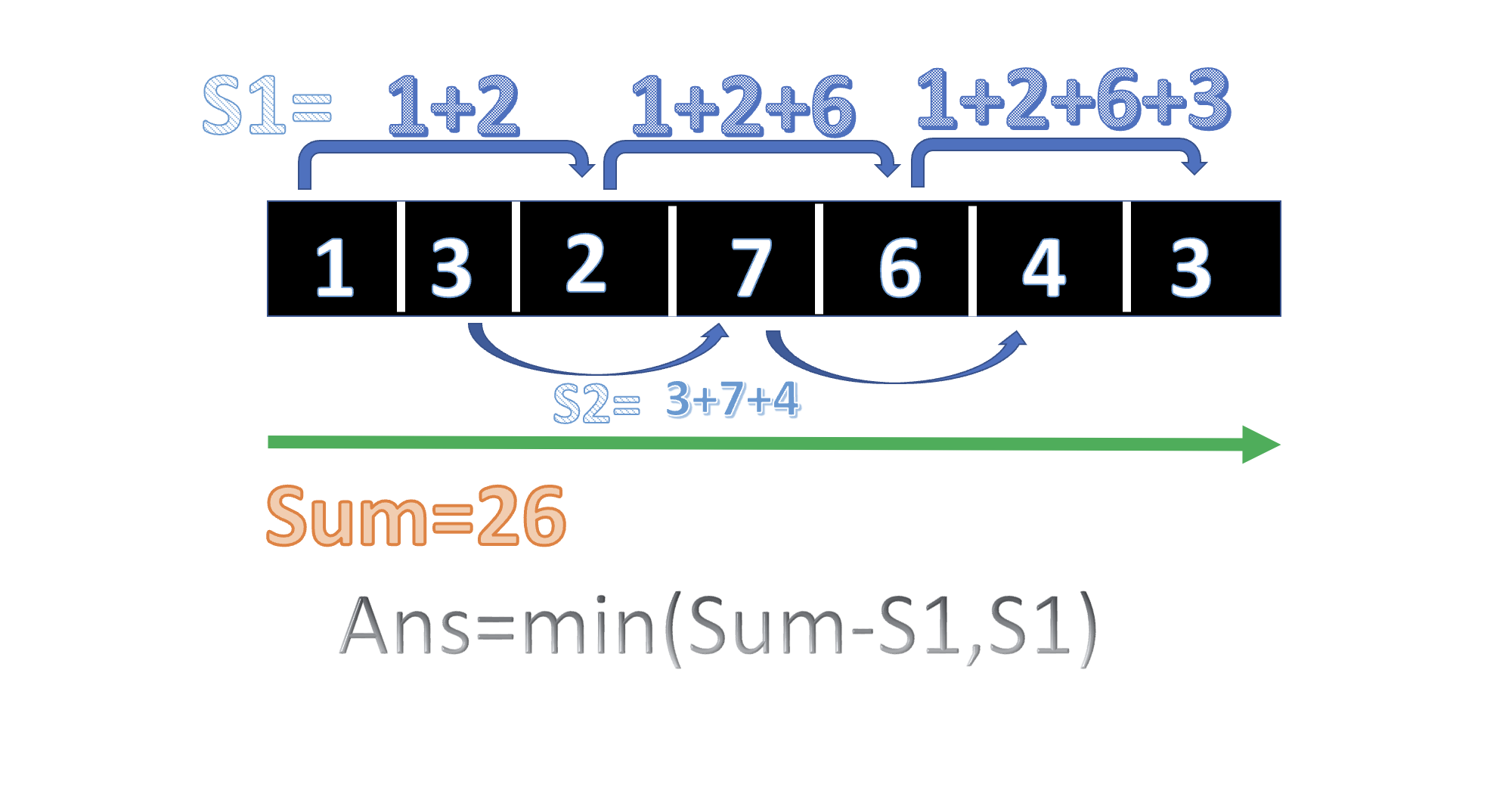
• Time Complexity : O(N)

Pseudo Code

Sum of array [0 to n-1]
Sun of the adjacent element from [0 to n-1]
print min(Sum-Sum_of_adjacent,Sum_of_adjacent)