Join Us
Loading Similar Posts
Entering edit mode
Question 1
Primes in Subtree
Click here to Practice
Submit Problem to OJ
Question 2
VM Pricing
Click here to Practice
Submit Problem to OJ
Question 3
Maximum Difference
Click here to Practice
Submit Problem to OJ
Entering edit mode
Solution for VM Pricing
Analysis
In the question it is mentioned that we are given an array of pairs (num_instances, price_per_instance) which basically represent the number of instances, and the price per instance when that number of instances are ordered. It is also given that points for which price per instance is negative/zero, they are to be disregarded. Then we need to interpolate the price per instance based on the number of instances given to us.
So, firstly we remove all points which have negative/zero price per unit instance. Then if there is only one point remaining in the array, then that will be the answer. Otherwise, we sort the array after which we look for the nearest points to the given instances. We can think of instances being on the x-axis and price per instance being on the y-axis. So for the given number of instances, we find the point which is just before this number of instances on the x-axis, and the point which is just after this number of instances on the x-axis.
Find the smallest x > x1 and largest x < x1,
where x1 is the given number of instances and x is the number of instances in the given array
So then we can think of these 2 points as a line and interpolate the price per unit instance. A diagram for the same can be seen below:
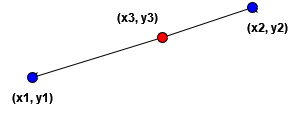
Here (x1, y1) and (x2, y2) are the points closest from the left and from the right respectively to the query instances x3. Our aim is to find x3.
However, in case all points are greater than the query x3, we need to take the closest 2 elements which are greater than the query instance. The diagram can seen below:
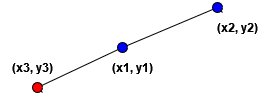
Similarly, if all points are smaller than the query x3, we need to take the closest 2 elements which are smaller than the query instance.
Now, in all these cases we can find out the slope of the line from the 2 points, and then calculate y3 using the slope and x1, x3, since (y2-y1)/(x2-x1) = (y3-y1)/(x3-x1)
Implementation
for(ll i=0;i < m;i++)
{
if(prices[i] < = 0)
continue;
points.pb({instances[i], prices[i]});
}
sort(points.begin(), points.end());
ll tot = points.size();
if(tot==1)
{
cout < < points[0].se < < '\n';
return;
}
auto it = lower_bound(points.begin(), points.end(), make_pair(n, (ld)INT_MIN));
if(it==points.end())
{
//everything is smaller
ld num = points[tot-1].se - points[tot-2].se;
ll den = points[tot-1].fi - points[tot-2].fi;
ll x_diff = n - points[tot-1].fi;
ld y_diff = (num * x_diff)/(den);
ld ans = y_diff + points[tot-1].se;
cout < < fixed << setprecision(6) < < ans < < '\n';
}
else if(it->fi==n)
{
cout < < it->se < < '\n';
return;
}
else if(it==points.begin())
{
ld num = points[0].se - points[1].se;
ll den = points[0].fi - points[1].fi;
ll x_diff = n - points[0].fi;
ld y_diff = (num * x_diff)/(den);
ld ans = y_diff + points[0].se;
cout < < fixed < < setprecision(6) < < ans < < '\n';
}
else
{
ll idx = it - points.begin();
ld num = points[idx].se - points[idx-1].se;
ll den = points[idx].fi - points[idx-1].fi;
ll x_diff = n - points[idx].fi;
ld y_diff = (num * x_diff)/(den);
ld ans = y_diff + points[idx].se;
cout < < fixed < < setprecision(6) < < ans < < '\n';
}
Entering edit mode
Solution to Primes in Subtree
Analysis
In the question it mentioned that we are given a graph consisting of n nodes and m edges. We are also given q queries, in each of which we are given a particular node, and we need to find the number of nodes in the subtree rooted at that node which are prime.
Now, the values of the nodes are in the range [1, 10^5] (given). So we can precompute which numbers in the range [1, 10^5] are prime, then do a DFS (Depth First Search) to calculate the total number of primes in the subtree rooted at each node. We recursively define the DFS as:
num[i] = num[j_1] + num[j_2] + num[j_3] + ... + num[j_k]
if i is prime:
num[i] += 1
Here num[i] represents the number of prime numbers in the subtree rooted at node i, and j_1, j_2, j_3, ...., j_k are the children of the node i. So, the number of prime numbers in the subtree rooted at node i is the sum of the number of primes in subtrees rooted at its children and plus 1 if the node i itself is a prime number.
Now, we can calculate for all numbers in the range [1, 10^5], whether they are prime or not by using Sieve of Erastothenes in O(nlogn) time complexity, and then do a DFS to calculate the answer for all nodes in O(n). Then each query can be answered in O(1).
Implementation
ll spf[100001] = {0};
map < ll,ll > primes;
void sieve()
{
for(ll i=1;i < = 100000;i++)
spf[i] = i;
for(ll i=2;i < = 100000;i++)
{
for(ll j=i*i;j < = 100000;j+=i)
{
if(spf[j]==j)
spf[j] = i;
}
}
for(ll i=2;i < = 100000;i++)
{
if(spf[i]==i)
primes[i] = 1;
}
return;
}
void dfs(ll root, vector < vector < ll > > &adj, vector < ll > &nums, vector< ll > &values, vector < bool > &visited)
{
ll ans = 0;
if(primes[values[root]])
ans = 1;
visited[root] = true;
for(auto u:adj[root])
{
if(visited[u])
continue;
dfs(u, adj, nums, values, visited);
ans += nums[u];
}
nums[root] = ans;
return;
}
Note: Though it is mentioned in the question that the number of edges can be less than n-1, so it can be a disconnected tree. For components not connected to the root 1, we assume that all the nodes have answer 0.
Entering edit mode
Solution to Maximum Difference
Analysis
In the question it is mentioned that we are given a graph, and for each connected component, we need to find the difference between the maximum and minimum value in that connected component. Then across all connected components we take the maximum of this value.
We can simply iterate from nodes 1 to n and do a BFS/DFS starting from each node that has not been previously visited. Then all nodes which occur in the BFS/DFS are nodes in this connected component and we can calculate their maximum and minimum in the BFS/DFS itself. Then we calculate the maximum - minimum value and take maximum over all components.
Since we are simply doing a DFS, the time complexity will be O(logn).
Implementation
pair < ll,ll > dfs(ll root, vector < bool > &visited, vector < vector < ll > > &adj)
{
visited[root] = true;
ll maxi = root;
ll mini = root;
for(auto u:adj[root])
{
if(visited[u])
continue;
pair < ll,ll > p = dfs(u, visited, adj);
maxi = max(maxi, p.fi);
mini = min(mini, p.se);
}
return {maxi, mini};
}
void solve()
{
ll n,m;
cin > > n > > m;
vector < vector < ll > > adj(n+1);
for(ll i=0;i < m;i++)
{
ll u,v;
cin > > u > > v;
adj[u].pb(v);
adj[v].pb(u);
}
vector < bool > visited(n+1, false);
ll ans = 0;
for(ll i=1;i < = n;i++)
{
if(visited[i])
continue;
pair < ll,ll > vals = dfs(i, visited, adj);
ans = max(ans, vals.fi - vals.se);
}
cout < < ans < < '\n';
return;
}
