Question: Sprinklr, Recently Asked Online Assessments, November, 2022 | Crayon Box

Entering edit mode

Question

Crayon Box

You are given a box of crayons with different colors represented by different alphabets. In one operation, you can remove several continuous crayons of the same color. You may perform this operation several times until the box is empty. Each time you can choose the crayon set. They must be continuous and of the same colors(i.e., set of x crayons, x>=1). After removing them, you will get x*x points.

You are given an integer N where N denotes the total number of crayons in the box. You are also given an array of colors denoting the N colors in the box, where each color is represented by an English alphabet.

Return the maximum points, you can get in the given scenario.

Constraints : N <= 60

Example 1-> colors array == [ a ,b , c , c , c , b , a ,b ,a]

Remove c ( + 9 ) -> [ a , b , b , a , b , a]
Remove a ( + 1 ) -> [ a , b ,b ,b , a ]
Remove b ( + 9 ) -> [ a , a ]
Remove a ( + 4 ) -> []
Ans -> 23

Example 2 -> colors array == [ a ,a , b , b , a , a ,c]

Ans -> 21

ADD COMMENT • link

Entering edit mode

Approach/Solution

The question is really hard and the constraints are also too low so we can expect a solution of N^4.
We are having 26 colours in total from a-z.
The question is a bit harder so will try to explain my best If Still not able to solve can try more Dynamic programming questions first.
Let DP(l, r, k) denote the maximum points we can get in boxes[l..r] if we have extra k boxes which are the same colour as boxes[l] on the left side.
For example : [b,b,a,b,b]
The DP(l=3, r=4, k=2) is the maximum points we can get in boxes[3..4] if we have extra 2 boxes the same colour as boxes[3] in the left side, it's the same as we find the maximum points in boxes = [b, b, b, b]
Since (a+b)^2 > a^2 + b^2, where a > 0, b > 0, it's better to greedy to remove all contiguous boxes of the same colour, instead of splitting them.
So we increase both l and k while boxes[l+1] == boxes[l]
Now, we have many options to consider:
Option 1: Remove all boxes which have the same as boxes[l], total points we can get is Dp(l+1, r, 0) + (k+1)*(k+1) (k left boxes and the lth box have the same colour)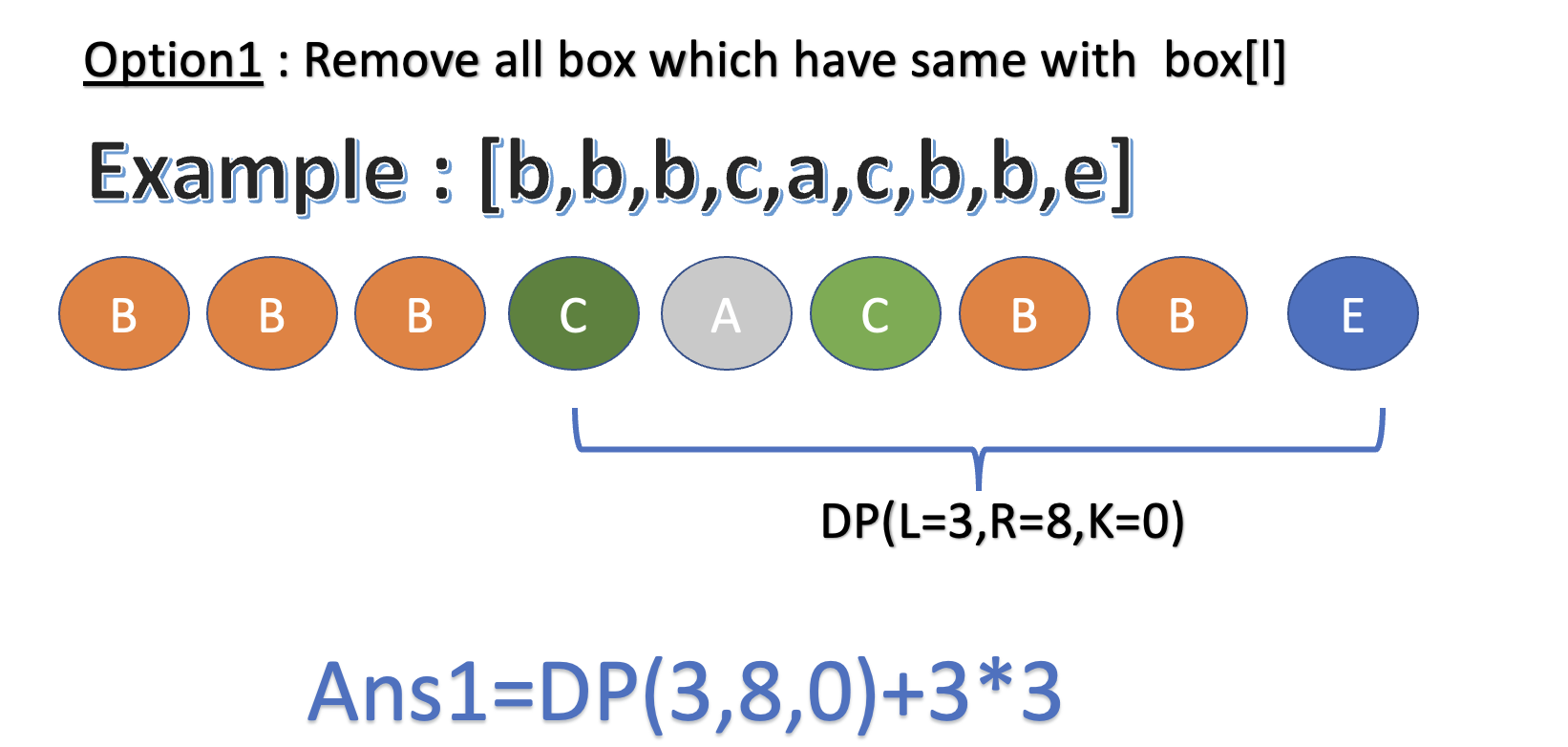
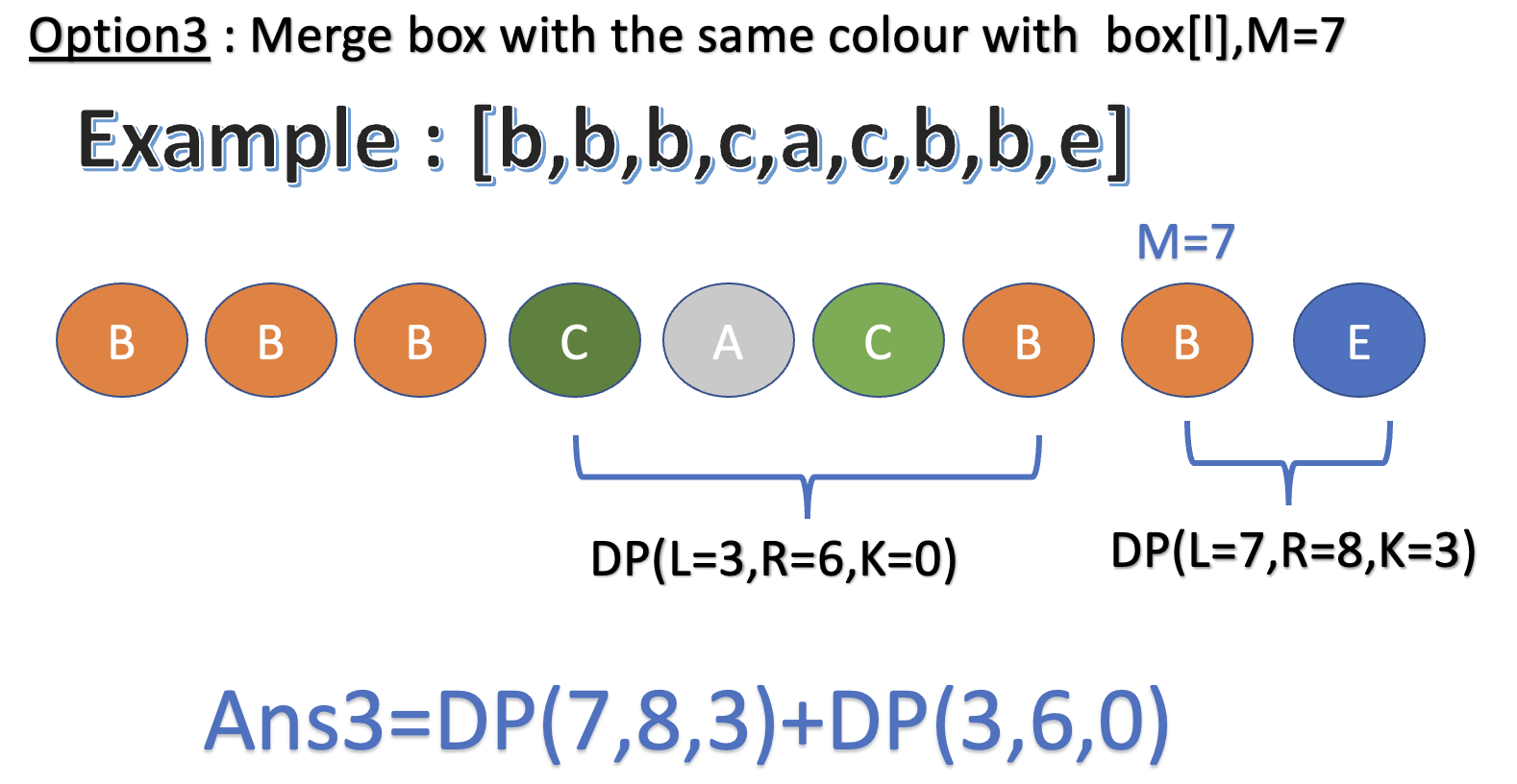
Other options we try to merge non-contiguous boxes of the same colour together, by finding the index j, where l+1 <= j <= r so that boxes[j] == boxes[l].
Total points we can get is dp(j, r, k+1) + dp(l+1, j-1, 0)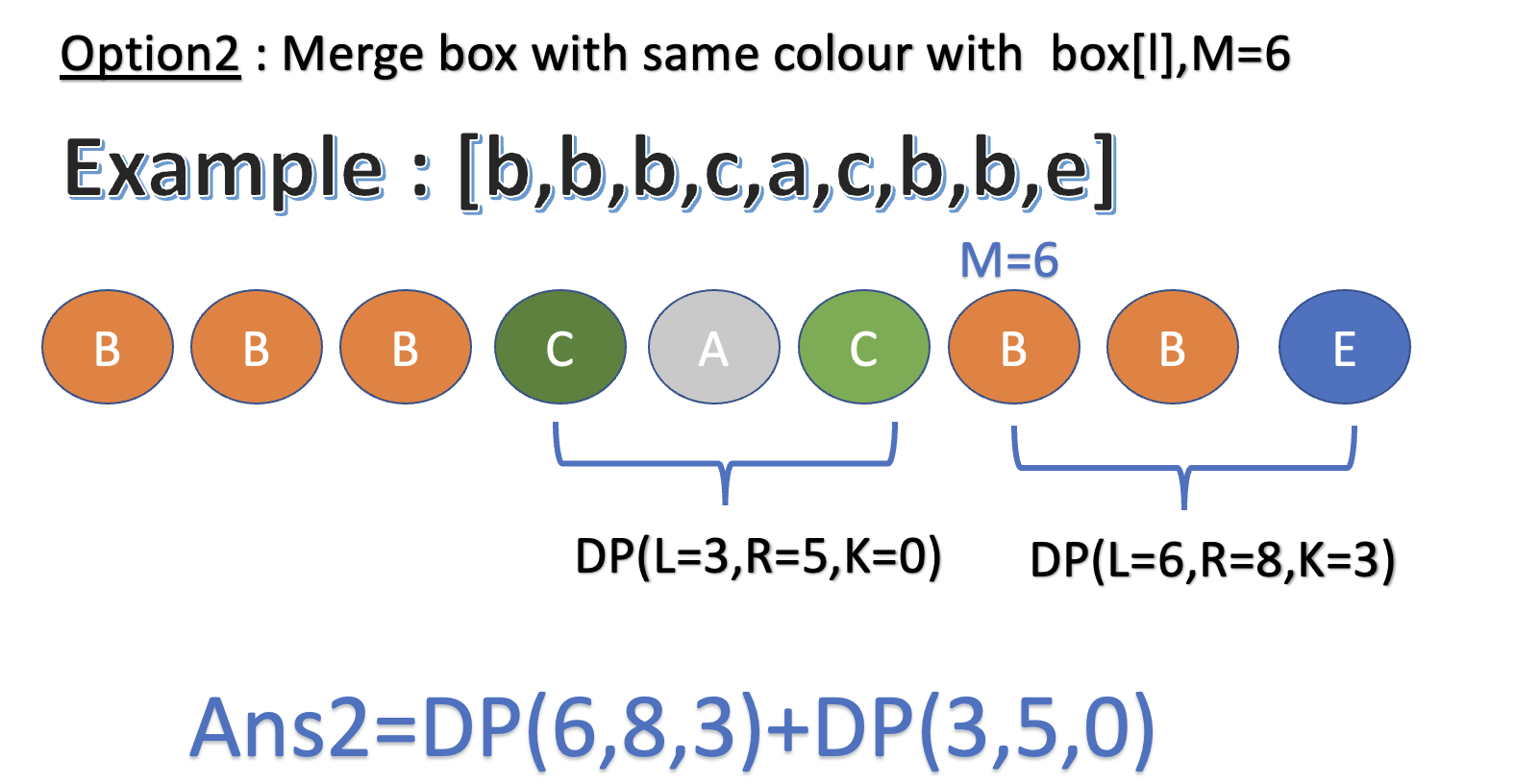
Choose the option which has the maximum score we can get.
Time Complexity : O(N^4) Space Complexity : O(N^3)

Pseudo Code

int Dp[N+5][N+5][N+5]
int dp(vector&lt;int&gt;&amp; boxes, int l, int r, int k) {
     if (l &gt; r) return 0;
    if (memo[l][r][k] &gt; 0) return memo[l][r][k];
    int lOrg = l, kOrg = k;

    while (l+1 &lt;= r &amp;&amp; boxes[l] == boxes[l+1]) { // Increase both `l` and `k` if they have consecutive colors with `boxes[l]`
        l += 1;
        k += 1;
    }
    int ans = (k+1) * (k+1) + dp(boxes, l+1, r, 0); // Remove all boxes which has the same with `boxes[l]`
    for (int m = l + 1; m &lt;= r; ++m) // Try to merge non-contiguous boxes of the same color together
        if (boxes[m] == boxes[l])
            ans = max(ans, dp(boxes, m, r, k+1) + dp(boxes, l+1, m-1, 0));
    return memo[lOrg][r][kOrg] = ans;
 }