9 weeks ago

John 910

Hyderabad

Question 1

Mother Vertex

You are given a directed graph with A vertices and M edges.

You are given an array B with dimensions M x 2, where each row denotes a directed edge from Bi, 0 to Bi, 1.

You need to find if there exists a mother vertex in the given graph. Return 1 if it exists, otherwise 0.

A mother vertex is defined as a vertex from which all the vertices in the graph are accessible by a directed path.

Problem Constraints

• 1 <= A <= 10^5
• 1 <= M <= 2 * 10^5
• 1 <= Bi,0, Bi,1 <= A

There can be duplicate edges or self loops in the input graph.

Input Format

The first argument is the integer A. The second argument is the 2D integer array B.

Output Format

Return a single integer 1 if a mother vertex exists, otherwise 0.

Example

Input 1:

A = 3
B = [[1, 3], [2, 3], [1, 3]]

Output 1:

0

Input 2:

A = 3
B = [[1, 3], [2, 3], [3, 2]]

Output 2:

1

Example Explanation

Explanation 1:

There is no vertex from which all the other vertices are accessible.

Note there can be duplicate edges.

Explanation 2:

Vertex 1 is the mother vertex. We can reach 2 using 1 -> 3 -> 2. We can reach 3 using 1 -> 3

Question 2

Set Matrix Zeros

Given a matrix, A of size M x N of 0s and 1s. If an element is 0, set its entire row and column to 0.

Note: This will be evaluated on the extra memory used. Try to minimize the space and time complexity.

Input Format:

The first and the only argument of input contains a 2-d integer matrix, A, of size M x N.

Output Format:

Return a 2-d matrix that satisfies the given conditions.

Constraints:

• 1 <= N, M <= 1000
• 0 <= A[i][j] <= 1

Examples:

Input 1:

[   [1, 0, 1],
    [1, 1, 1], 
    [1, 1, 1]   ]

Output 1:

[   [0, 0, 0],
    [1, 0, 1],
    [1, 0, 1]   ]

Input 2:

[   [1, 0, 1],
    [1, 1, 1],
    [1, 0, 1]   ]

Output 2:

[   [0, 0, 0],
    [1, 0, 1],
    [0, 0, 0]   ]

Question 3

Array Sum

You are given two numbers represented as integer arrays A and B, where each digit is an element.

You have to return an array which representing the sum of the two given numbers.

The last element denotes the least significant bit, and the first element denotes the most significant bit.

Constraints

• 1 <= |A|, |B| <= 10^5
• 0 <= Ai, Bi <= 9

Input Format

The first argument is an integer array A. The second argument is an integer array B.

Output Format

Return an array denoting the sum of the two numbers.

Example

Input 1:

A = [1, 2, 3]
B = [2, 5, 5]

Output 1:

[3, 7, 8]

Input 2:

A = [9, 9, 1]
B = [1, 2, 1]

Output 2

[1, 1, 1, 2]

Explanation 1:

Simply, add all the digits in their place.

Explanation 2:

991 + 121 = 1112

Note that the resultant array size might be larger.

20 days ago

Lokesh 310

Hyderabad

Question 1: Mother Vertex

Overview:

• Given a directed graph G(V, E), find whether a mother vertex exists or not.

mother vertex

• Is a vertex from which there is a path to all other vertices

Approach:

• Do DFS on the graph, and store the order of DFS query exits.

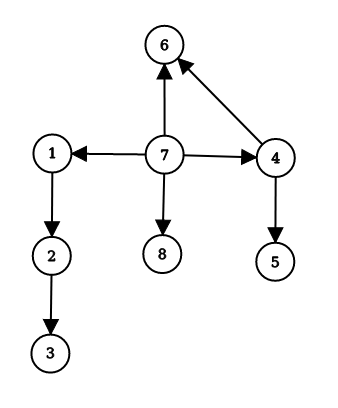
• In the image above:
  • First DFS call at vertex 1.
    • order of start of DFS [1,2,3].
    • order of exits of DFS [3,2,1].
    • Visited nodes [1,2,3]
  • Second DFS call from vertex 4.
    • order of start of DFS [4,5,6].
    • order of exits of DFS [5,6,4].
    • Visited nodes [1,2,3,4,5,6]
  • Third DFS call from vertex 7.
    • order of start of DFS [7,8].
    • order of exits of DFS [8,7].
    • Visited nodes [1,2,3,4,5,7,8]
  • Combined order of exists [3,2,1,5,6,4,8,7].
• The argument now is if there are mother vertices, then the last vertice in combined order of DFS exits is one of them
  • Last exited vertex(X) will be a vertex from which the last root DFS call was made.
  • All vertex visited before this last root DFS was called don't have a path to X, meaning none of those are mother vertices
  • If the X is not a mother vertex, all vertices visited due to the root DFS call of X cannot be the mother vertex, as they don't have paths to all other vertices. If they had, then X would be a mother vertex in the first place
• Find the exit order of DFS calls and check whether the last vertex in that order is a mother vertex. If yes, output 1, else 0

Complexity:

• O(N+M) N is the number of vertices, and M is the number of edges.

PseudoCode:

vector<bool> vis(1000001, false);
vector<int> adj[1000001];
vector<pair<int, int>> edges;
vector<int> order;
void DFS(int n)
{
    vis[n] = true;
    for (int i = 0; i < adj[n].size(); i++)
        if (!vis[adj[n][i]])
            DFS(adj[n][i]);
    order.push_back(n);
}
bool motherVertex(vector<pair<int, int>> edges, int n)
{
    for (int i = 0; i < edges.size(); i++)
        adj[edges[i].first].push_back(edges[i].second);

    for (int i = 1; i <= n; i++)
        if (!vis[i])
            DFS(i);
    for (int i = 1; i <= n; i++)
        vis[i] = false;

    int x = order[order.size() - 1];
    order.clear();
    DFS(x);

    if (order.size() == n)
        return 1;
    return 0;
}

8 weeks ago

Akash 240

New Delhi

Question 3: Array Sum

Overview

• Given two elements represented as arrays, return their sum in the form of an array

Approach

• Traverse both the arrays from the end till we reach the 0th index of either of the array and while traversing, add the elements of both arrays along with the carryover sum from the previous sum. Then store the unit digit of the sum and forward the carryover for the next index sum. While adding the 0th index element, if the carry is left, then append it to the beginning of the number.
• For example, A[] = { 1, 2, 3} and B[] = { 2, 5, 5 } represent 123 and 214 respectively. So the sum of both numbers is 378.

Complexity

O(N), N is the size of the given array.

17 months ago

Rishabh Verma 170

question 2: Set Matrix Zeroes

Overview:

• make the element 0 if any element in the same row or column is 0.

Approach:

• First make two arrays Row and Column to keep track of zeroes.
• then iterate over every element if any element A[i,j] is 0 then mark R[i] and C[j] to 1.
• At last iterate over every element, check if row or column array is 1, if found then change it to 0 else leave it 1.

Complexity:

• O(M*N) where N is number of columns and M is number of rows.

Pseudo Code

void Solve() {
  int n,m;
  cin>>n>>m;
  bool row[n],col[m];
  // setting intial values of rows and columns to 0
  fill(row,row+n,0);
  fill(col,col+m,0);
  int input;
  for(int i=0;i < n;i++){
    for(int j =0;j < m;j++){
      cin>>input;
      if(input==0) row[i]= 1,col[j]= 1; 
      // to keep a track whether any row or column contains 0.
    }
  }
}