9 weeks ago

John 910

Hyderabad

Qualcomm Interview Experience for Associate Software Engineer Position

Basic discussion on resume and current company's tech stack and project was common in all rounds.

Round1

• Discussion on time and space complexity.

Q1. Find missing smallest positive number in unsorted integer array.

{1,5,6,-2,4,2}, smallest positive number : 3

• Was asked definition of complete binary tree.

Q2. Convert linked list to complete binary tree.

Input

1->2->3->4->5->6

Output

      1
     / \
    2   3
   /\   /\
  4  5 6

• Was also asked what is MVC architecture.

Round2

• Discussion on OOPS Concepts.
• Interviewer also asked about design patterns in Java.

Q1. Check for balanced parenthesis in a string.

Q2. Attaching Screenshot for it.

Round3

• Discussed about singleton class in Java.
• Interviewer asked about dependency injection.
• Unit Testing.

Q1. Print nth fibonacci number- both recursive and iterative.

Q2. Second most repeated char in a string

Input

nkslanfaaboutcec

Output

After the 3rd round there was a basic feedback sort of a round with a different interviewer.

Interviewer also asked why you want to switch and some other basic questions.

Also asked where do you want to see yourself in 3-4 years.

Then the interviewer said that Qualcomm Hyderabad works in sync with Qualcomm Seattle (or San Diego he said I guess), so there will be another interview round of 1 hour max with the Seattle team as well either on Friday or Monday.

Qualcomm Seattle Round

Interviewer asked few basic question related to resume and career like-

• What was the most challenging task done till now in the current company?
• How any of the unknown requirements were handled in any of the projects mentioned in the resume?
• Are you aware about agile practices?

Next moved on to coding questions-

Q1.

Find the uncommon elements in two unsorted arrays.

Input1:

[3 4 2 3 4] 

Input2:

[3 6 3 2 1 1] 

Output:

[4 6 1]

I told him the brute force approach for this and moved on to the hashing based approach and coded it.

Q2.

Given a maze represented by a two dimensional arrays with R rows and C columns. Find a path from start position to exit.

You cannot move diagonally between cells.

Passable cells are marked with a period .

Impassable cells are marked with a hash #

The start position is at cell S

The exit is at cell E

For example:

###...##..
....#....#
#..###.#.#
S#.#.#.#..
...#...E#.

I applied DFS over here similar to what was used in the athletic arena problem and he was satisfied by this approach.

23 months ago

Harsh Priyadarshi 70

Question1 (Round 3)

Overview

• To print the Nth fibonacci number from the fibonacci sequence.

Approach

• We have a simple recurrence relation, F(n)=F(n-1)+F(n-2)
• This will take exponential time to calculate.
• We can speed up the process using Dynamic Programming.

PseudoCode

vector <int> dp(n+1);
    dp[0]=0;
    dp[1]=1;
    for(int i=2;i<=n;i++){
        dp[i]=(dp[i-1]%mod+dp[i-2]%mod)%mod;
    }

Complexity

• O(n)

Note

• Take care of overflows

8 weeks ago

Akash 240

New Delhi

Question 1: Missing Smallest Positive Number

Overview

• Find the missing smallest positive number in an unsorted integer array.

Approach

• The idea is to mark the elements in the array which are greater than N and less than 1 with 1.

• The smallest positive integer is 1. First, we will check whether 1 is present in the array. If it is not present, then 1 is the answer.

• If present, then, again, traverse the array. The largest possible answer is N+1, where N is the size of the array.

• When traversing the array, if we find any number less than 1 or greater than N, change it to 1. This will not change anything, as the answer will always be between 1 to N+1.

• Now, our array has elements from 1 to N. Now, for every ith number, increase arr[(arr[i]-1)] by N. But this will increase the value more than N. So, we will access the array by arr[(arr[i]-1)%N].

• We will now find which index has a value less than N+1. Then i+1 will be our answer.

Complexity

Time Complexity: O(N), N is the size of the array.

8 weeks ago

Akash 240

New Delhi

Round 2 Question 1: Valid Parentheses

Overview

• Check if the parentheses sequence is balanced or not.

Approach

• An input string is valid if: Open brackets must be closed by the same type of brackets.

Open brackets must be closed in the correct order.

// Initialize a stack and a index idx = 0... 
stack<char> stack;
int idx = 0; 
// If the string is empty, return true... 
if(s.size() == 0){ 
   return true; 
} 
// Create a loop to check parentheses... 
while(idx < s.size()){ 
// If it contains the below parentheses, push the char to stack... 
     if( s[idx] == '(' || s[idx] == '[' || s[idx] == '{' ){ stack.push(s[idx]); } 
     // If the current char is a closing brace provided, pop the top element... 
     // Stack is not empty... 
     else if ( (s[idx] == ')' && !stack.empty() && stack.top() == '(') || (s[idx] == '}' && !stack.empty() && stack.top() == '{') || (s[idx] == ']' && !stack.empty() && stack.top() == '[') ){ 
        stack.pop(); 
     } 
     else { 
        return false;       // If The string is not a valid parenthesis... 
     } 
     idx++;      // Increase the index... 
 } // If stack.empty(), return true... 
if(stack.empty()) { 
    return true; 
} 
return false;

Complexity

Time Complexity: O(|S|)

19 months ago

Gigaliths 570

IIT Ropar

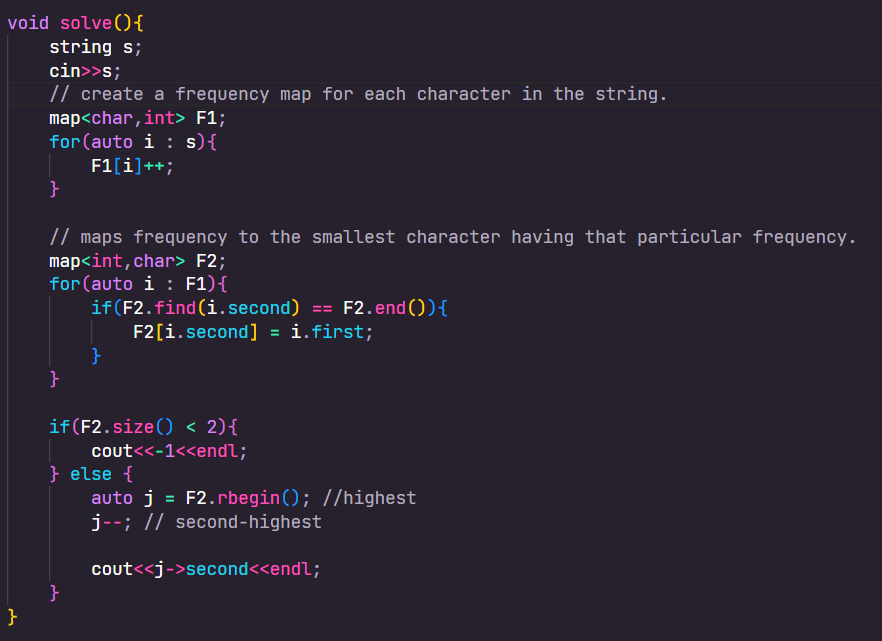
Solution : Round 3 - Question 2

Overview

• We are given a string containing ASCII characters.
• We need to find the second most occurring character in the given string.
• If there are multiple such characters, we need to prefer the character with lower ASCII value.

Approach

• We need to first find the number of occurrences of each character. We will use a hashmap to maintain the same.
• Lets define a hashmap F1 (char->int) to maintain the frequency of each character while you traverse the string.
• Use this hashmap F1 (char->int) to create a new hashmap F2(int->char) of frequencies mapped to smallest ASCII character having that particular frequency.
• Find the second highest key in F2 and print the character mapped associated to that frequency.
• If size of F2 < 2 , this means that there isn't a second-highest frequency ( we print -1)

Example

• string = "aaabbccfed"
• F1 = {a:3 , b:2 , c:2 , d:1 , e:1 , f:1}
• F2 = {1:d , 2:b , 3:a}
• Second largest key in F2 = 2
• Print(F2[2]) == 'b'

Complexity

• O(N) time complexity to traverse the array
• O(1) space , since the number of ASCII characters in a string is constant.

Code

21 months ago

hardik kapoor 130

Qualcomm Seattle round Q2

Approach

• We can just do BFS (breadth first search) from 'S'.
• If we can reach 'E', output is "YES", else "NO".
• For outputting the path, we can store parent in each iteration of bfs, and backtrack from 'E'.

C++ Code

vector<int> dx={1,-1,0,0};
vector<int> dy={0,0,1,-1};

int solve(vector<string> v)
{
    int n=v.size(),m=v[0].size();
    int sx=-1,sy=-1,ex=-1,ey=-1;
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
        {
            if(v[i][j]=='S')
            {
                sx=i,sy=j;
            }
            if(v[i][j]=='E')
            {
                ex=i,ey=j;
            }
        }
    }
    queue<pair<int,int>> q;
    q.push({sx,sy});
    vector<vector<int>> vis(n,vector<int>(m,0));
    vector<vector<pair<int,int>>> par(n,vector<pair<int,int>>(m,{-1,-1}));
    vis[sx][sy]=1;

    while(!q.empty())
    {
        auto x=q.front();
        q.pop();
        for(int l = 0;l < 4;l++)
        {
            int ni=x.first+dx[l],nj=x.second+dy[l];
            if(ni < 0||ni >= n||nj < 0||nj >= m)
                continue;
            if(v[ni][nj]=='#'||vis[ni][nj]==1)
            {
                continue;
            }
            par[ni][nj]=x;
            q.push({ni,nj});
            vis[ni][nj]=1;
        }
    }
    if(par[ex][ey]!=(pair<int,int>){-1,-1}){
        vector<pair<int,int>> path;
        path.push_back({ex,ey});
        pair<int,int> curr={ex,ey};
        while(curr!=(pair<int,int>){-1,-1})
        {
            curr=par[curr.first][curr.second];
            if(curr!=(pair<int,int>){-1,-1})
                path.push_back(curr);
        }
        reverse(path.begin(),path.end());
        for(auto x:path)
            cout<<x.first<<" "<<x.second<<endl;
    }
    return par[ex][ey]!=(pair<int,int>){-1,-1};
}

Time Complexity : O(N*M)

8 months ago

Shikhar Mehrotra 480

Chennai

Seattle Round Q1

Solution

• The question can be solved by iterating over each elements of array and check whether it occurs in another array or not.
• Searching whether an element occurs in another array can be done in O(N)time by bruteforce, and can be optimized by maintaining a HashMap of the array for doing it in O(1) time.
• We should also keep a track of whether an element is not repeated in the answer , again it could be also done using HashMap in O(1) time.